HY03

HY03

저는 전문가가 아니고 이것 저것 알아보는 비전문가 입니다.
틀린 내용이 기술되어도 너그러이 봐주시고 댓글을 남겨주셨으면 좋겠습니다.

Fundamentals of Reinforcement Learning - 01. Week 1

Course Introduction

  • Supervised Learning (지도학습)
    • 학습자가 답이 기입되어 있는 라벨링된 예시에 접근함
    • 정답이 무엇이었는지 말해주는 선생이 존재
    • 학습데이터 : 정답 (혹은 정답인 동작) 을 가르쳐주는 정보를 학습한다.
    • 피드백 : 취해야 할 올바른 조치를 나타낸다. (이번 행동이 얼마나 좋았는지는 알려주지 않는다.)
      • 피드백은 행동에 대해 완전 독립적.
  • Unsupervised Learning (자율학습)
    • 데이터 기저에 있는 구조를 추출 (데이터 표현법)
      • 이 데이터 표현법은 지도학습이나 강화학습에 도움을 줄 수 있음
  • Reinforcement Learning (강화학습)
    • 학습자에게 최근의 행동에 대한 보상을 제공함
    • 좋은행동이 어떤것일지 식별해주는 환경이 존재하나 정확히 어떻게 해야하는지는 알려주지 않음
    • 지도학습이나 자율학습을 통해 일반화 (Input 이 달라져도 출력성능에 영향을 주지 않음) 를 개선할 수 있음
    • 바뀌는 환경속에서 상호작용하며 학습하는 것에 주안점을 둠
      • 학습자가 단순히 반복되는 환경에서 계산을 통해 좋은 행동이 무엇인지 학습하는 것이 아님.
      • 학습자가 시행착오를 통해 변화하는 환경에서 목표를 바꾸어 가며 더 잘하는 것을 추구
    • 학습데이터 : 행동을 수행한 것에대한 평가를 학습한다.
    • 피드백 : 이번 행동이 얼마나 좋았는지를 피드백한다. (그것이 최선/최악인지는 알 수 없다)
      • 피드백은 행동에 완전 종속됨.
      • 때문에 최선의 행동을 찾아 끊임없이 탐험해야 함.

관련 자료 (RLbook2018 Pages 25-36)

  • 용어설명
    • Stationary (정상성) Probability : 여러 시간 구간마다 통계적 성질이 동일한 것
      • 예) 주사위 던지기 : 시간에 무관하게 동일한 확률값
    • Non-Stationary (비정상성) Probability : 시간에 따라 통계적 성질이 변하는 것
      • 예) 변덕스러운 날씨, 기후 등
    • Nonassociative setting : 다른 Action(행동), 다른 Environment(환경) 을 가정하지 않는 세팅
      • full reinforcement learning problem 의 복잡성을 배제 (다양한 환경, 비정상성, 행동의 보상이 즉각적이지 않음 - 현실세계)
      • 이미 환경이 어떠한 피드백을 줄지 알고 있다.
  • Multi-armed Bandits
    • 간단한 세팅 환경 (K-armed bandit problem 의 단순화 버전)
      • 한가지 이상 상황에서의 동작을 학습하는 것을 배제 (Nonassociative setting)
      • 목적1 : 평가 피드백 (Evaluative feedback) 이 정답을 알려주는 피드백 (Instructive Feedback) 과 어떻게 다른지 확인
      • 목적2 : 둘이 결합될 수 있는지 확인
    • 목표
      • 기초적 학습법 (Learning methods) 안내
      • 이 Bandit problem 이 associative (연관성) 성질을 가지게 되었을 때 어떻게 변할지 확인
    • A k-armed Bandit Problem
      • 문제에 대한 설명
        • 반복적으로 k 개의 다른 옵션/행동을 선택
        • 각 선택 마다 보상 (선택한 행동에 따른 정상성 확률 분산을 가진 보상) 을 받는 문제
        • 목적 : 특정 기간동안 최대한의 보상을 받는 것
      • 문제에 대한 예시 1
        • 슬롯머신 혹은 “one-armed bandit” 문제와 동일하나 단지 레버가 k 가임.
        • 각 행동은 여러 대의 슬롯머신 중 한 대의 레버를 당기는 것과 동일
        • 가장 이익을 극대화 할 수 있는 레버에 집중하여 보상을 많이 받는 것이 목표
      • 문제에 대한 예시 2
        • 의사가 심각한 질병의 환자에게 실험적 치료들 중 하나를 선택
        • 보상 : 환자의 생존/ 치유율

      • 수식설명

        2_1_1_value_of_action

        • 위 수식은 문제를 풀었을 때 ($q_*$) 의 value of the action 에 대한 수식이다.
        • value of the action : 각각의 k 행동들이 가지는 기대/평균 보상값
        • $A_t$ : time-step $t$ 시점에 선택한 action
        • $R_t$ : $A_t$ 에 상응하는 보상
        • $q_*(a)$ : $a$ 가 선택되었을때 기대되는 보상값
        • $\doteq$ : is defined as
        • If you knew the “value of the each action” : 해당 문제를 풀었다고 볼 수 있음.
        • $Q_t(a)$ : $q_*(a)$ 와 유사한 값 (중간값)
        • $q_*$ 값은 에이전트가 알고 있는 값이 아님
      • greedy actions
        • action value 를 계속 추정하다 보면 어느 시점에서나 적어도 하나의 가장 큰 예측값을 가지는 action 이 존재
        • 이것을 greedy actions 라고 함.
        • 이 greedy action 을 선택하는 것 : 현재 알고 있는 values of the action 값을 exploiting 한다.
        • 이 greedy action 을 선택하지 않는 것 : 현재 exploring 중이라고 한다.
        • Exploitation (이기적 이용)
          • 현 step 에서 예측되는 보상값을 최대화 하는 옳은 방법
        • Exploration (탐색)
          • 장기 관점으로 보았을 때 이쪽의 보상 총합이 더 클 수 있음
      • Balancing exploration and exploitation
        • k-armed bandit 과 이와 유사한 문제의 특정 수학적 공식에 대해 탐색과 이용의 밸런스를 맞출 수 있는 정교한 방법이 존재
          • 하지만 이런 방법들은 정상성에대한 강한 가정을 전재하고, full reinforcement learning 환경이나 어플리케이션을 침해하거나 증명할 수 없는 사전지식을 이용한다.
          • 즉 활용 불가. (Full reinforcement learning 환경에서 이 밸런스 문제는 도전적인 과제임)
        • k-armed bandit problem 에서는 균형에 대해서만 고려하고, 단순 Exploitation 하는 것보다 균형을 맞춘 방식이 더 잘 작동한다는 것을 증명할 것임.
    • Action-value Methods
      • 행동 선택을 위해 행동(Action) 에 대한 가치를 측정하는 방법을 통상 Action-value method 라 한다.

      • 수식설명 1

        2_2_1_averaging_the_rewards

        • 위 수식은 action-value method 중 보상평균값으로 추정하는 방식에 대한 수식이다.
        • Action-value 는 통상적으로 해당 Action 이 선택되었을 때 보상 값의 평균치를 말한다.
        • 1(predictate) 는 행위를 하였을 때는 1, 아닌 경우 0 (가상의 1/0, 횟수의 개념)
        • 분모가 무한하게 커지면 $Q_t(a)$ 의 값은 $q_*(a)$ 의 값에 수렴한다.
        • 이 방식을 sample-average method 라 부르며, 이는 Action-value 를 구하기 위한 많은 방법 중 하나이다.

      • 수식설명 2

        2_2_2_greedy_action_selection_method

        • 위 수식은 greedy action selection method 에 대한 수식이다.
        • action selection 에서 가장 단순한 방법은 가장 큰 예측값에 해당하는 action을 선택하는 것이다.
        • 현 시점 이전까지 가장 탐욕적인 action 으로 정의된 행동을 하는 것.
        • $\underset{a}{\arg\max}$ : 후술되는 값이 최대값이 되는 action $a$ 를 의미
        • Greedy action selection 은 현 지식을 이용해 당장의 보상을 최대화 하는 방식
        • 정말 더 나은 방식을 찾기 위해 열등한 방식을 샘플링하는데 시간을 할애하지 않음.
      • $\varepsilon$-greedy methods
        • 위와 다른 대안으로 대부분 탐욕스러운 행동을 하되
        • 아주 작은 확률($\varepsilon$)로 action-value 와 관계 없이 균등한 확률로 $a$ 를 선택하는 방법이 있음.
        • 이 방법을 통한 샘플링 횟수가 무한하게 커지면 $Q_t(a)$ 의 값은 $q_*(a)$ 의 값에 수렴한다.
        • 이것은 점근적인 보장일 뿐, 실질적인 효과에 대한 것은 아니다.
  • The 10-armed Testbed

    • 조건 설명

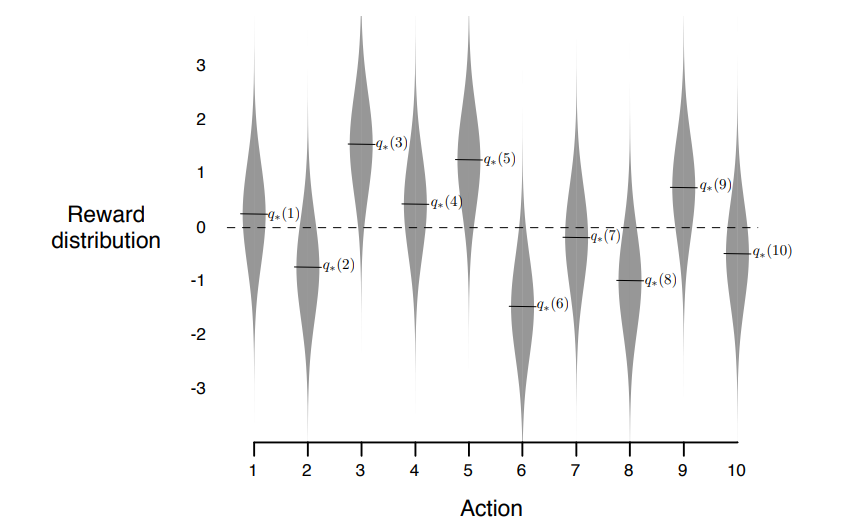
      2_3_1_10_armed_testbed

      • 10-armed testbed 의 bandit problem 문제 예시
      • 각 10 개 action 의 true value $q_*(a)$ 값 은 평균 0, 분산 1 인 정규분포 (표준정규분포) 를 따른다.
      • 위 조건으로 2000번의 서로 다른 bandit problem 을 수행, 평균 값을 취함.

    • 결과

      2_3_2_result_10_armed_testbed

      • 보상의 분산이 클수록 더 많은 탐험이 필요하며 $\varepsilon$-greedy methods 가 greedy methods 보다 더 잘 작동한다.
      • 만약 보상의 분산이 0이라면 각각의 action 후에 true value 값을 바로 알 수 있게 된다.
      • 위의 경우 greedy methods 가 더 잘 작동하게 된다. (탐험할 필요가 없음.)
      • 그러나 이런 결정론적인 상황에서도 몇가지 가정이 불확실하다면 탐험하는 쪽이 유리하다.
        • 비정상성 환경 (시간에 따라 true action-value 가 변함.)
        • 즉 Reinforcement learning 은 탐색과 이용에 균형이 필요함.
  • Incremental Implementation
    • action-value methods 를 획득한 보상의 평균 값으로 추정한다.

    • 이 경우 어떻게 전산화 하여 계산할지?

      2_4_1_estimated_value_of_single_action

      • 특정 단일 Action 에 대한 Action-value 를 예측, action 은 $n-1$ 번 선택됨.
      • 위 명확한 계산법은 모든 이전 기록을 가지고 있어야 하고, 예측값이 필요할 때마다 계산해야함.
        • 메모리가 많이 필요하고 연산량이 상당해진다.
        • 위의 방법이 아니라 이전 평균값에서 이번 보상값을 업데이트 하는 방식을 취하는 것이 효율적이다.

      2_4_2_update_action_value

      • 위의 구현법을 이용하면 메모리는 $Q_n$ 과 $n$ 값만을 저장하고 있고, 작은 계산을 통해 매번 새로운 예측값을 구할 수 있음.

      2_4_3_update_action_value

      • 수식의 뜻은 위와 같음
      • Target - OldEstimate = error
        • 위 에러 값은 예측값이 Target 에 가까워질 수록 작아짐
        • Target 은 예측이 움직이기 원하는 방향을 가리킴
      • StepSize : 각 타임스텝마다 변하는 step-size parameter 이며, 이 책에서는 $\alpha$ 혹은 $\alpha_t(a)$ 로 나타낸다.

      2_4_4_simple_bandit_algorithm

      • 완성된 simple bandit algorithm
      • breaking ties randomly.. 동점 기록일 경우 랜덤하게 선택한다.
  • Tracking a Nonstationary Problem
    • 보상의 확률이 변하는 reinforcement learning 문제에서는 오랜 과거 보상보다 최근 보상에 비중을 더 두는 것이 설득력있다.

    • 이러한 방법 중 하나로 상수 파라미터 (a constant step-size parameter) 를 사용하는 것이 유명하다.

      2_5_1_constant_step_size_parameter

      • 위의 수식을 weighted average 라고도 하는데 각 가중치의 합이 1이 되기 때문이다.
        • $(1-\alpha)^n + \sum_{i=1}^n\alpha(1-\alpha)^{n-i} = 1$
      • $1-\alpha$ 값이 1보다 작기 때문에 승수가 커질수록 (이전 step 의 값일수록) 가중치 값이 decay 됨
      • 때로는 위 수식을 exponential recency-weighted average 라고도 함 (지수적 최근성 가중치 평균)
    • 때로는 step 별로 변동하는 step-size parameter 를 사용하는 것이 편할 때가 있음.
      • 예를 들어 $\frac{1}{n}$ step-size parameter (sample-average method) 는 충분히 큰 step 을 진행할 경우 true action value 로 수렴하는 것을 보장한다.

    • 확률적 근사 이론은 확률 1로 수렴을 보장하는 데 필요한 조건을 제공한다.

      2_5_2_conditions_required_to_convergence_with_prob1

      • 첫번째 조건은 초기 조건이나 무작위 변동을 극복할 수 있을 정도로 step-size 가 큰 것을 보장
      • 두번째 조건은 step-size 가 수렴을 확신할 정도로 충분히 작은 것을 보장
      • $\frac{1}{n}$ 은 이 두 조건을 모두 만족하나, 상수 step 파라미터는 두번째 조건을 충족하지 않아 가장 최근의 보상값에 의해 완전히 수렴하지 못하게 됨.
        • 이것은 비정상성 환경에서 필요한 내용이다.
      • 두 조건이 만족하더라도 매우 느리게 수렴하거나, 만족스러운 수렴율을 얻기 위해 파라미터를 튜닝해야 할 수도 있음.
      • 위 이론은 이론적인 내용에는 자주 사용되나, 실제 적용 환경에서는 잘 사용되지 않음.
  • Optimistic Initial Values
    • 위에 언급한 모든 방법들은 initial action-value estimates ($Q_1(a)$) 에 어느정도 영향을 받는다.
    • 통계적 표현으로 이러한 방식들은 biased by their initial estimates (초기추정치에 의해 편향된다) 라고 한다.
    • 예를 들어 sample-average methods 는 이 편향이 모든 action을 한 번 이상씩 수행했을 때 사라진다면
      • 액션 a=1 to k 에 대해 초기값 $Q(a)$, $N(a)$ 를 초기값으로 쓰고, 한 번이라도 a 가 시도되면 수식에 따른 값으로 변경
      • n 으로 나눌 때 0 으로 나눌 수 없으므로..
    • 상수 a 를 사용하는 경우 이 편향은 영구적이다. (시간의 흐름에 따라 점차 감소하지만)
      • 별도의 초기값 할당이 아니라 처음부터 수식을 사용하되, 수식 내 0번째 스텝의 값이 초기값임.
    • 장점 : 예상할 수 있는 보상 수준에 대한 사전지식을 제공하는 쉬운 방법
    • 단점 : 모든 매개변수를 0 으로 설정하는 경우 사용자가 반드시 파라미터를 선택해야 한다.
    • 간단한 탐색 장려의 방법 : 초기 값을 0 대신 +5 로 설정 (10-armed testbed 상황으로 가정)
      • 초기값 +5 의 값은 매우 낙관적인 수치
      • 특정 action 을 선택하고 받는 보상 값이 예측치보다 작음 (disappointed with the rewards)
      • 학습자는 다른 action 을 선택하게 되고 이 상황을 몇번 반복됨. (greedy action 일지라도…)

      2_6_1_optimistic_greedy

      • 10-armed bandit testbed 에서 greedy method 를 초기값 $Q_1(a) = +5$ 로 세팅한 결과
      • 비교군은 $\varepsilon$-greedy method 에 초기값 $Q_1(a) = 0$
      • 이 trick 은 stationary problem 에서 꽤 효과적이나, 탐색을 장려하는 일반적인 방법은 아님.
      • 이러한 비판은 sample-average methods 에서도 통용된다.
        • 초기 시점을 특수한 이벤트로 여긴다.
        • 모든 보상을 똑같은 가중치로 평균을 구한다.
  • Upper-Confidence-Bound Action Selection
    • action-value 추정값의 불확실성 때문에 탐험은 반드시 필요하다.
    • greedy actions 는 현재 시점에는 가장 최적의 선택이나 다른 action 이 실제로는 더 좋은 것일 수 있다.
    • $\varepsilon$-greedy action selection 은 강제적으로 non-greedy action 을 선택하지만 선호도 없이 무차별적인 선택을 하여 greedy 한 선택을 하게 될 수도 있다.
      • 강제적인 선택을 할 때는 non-greedy 한 선택을 하는 것이 좋음
      • 추정치가 최대치에 얼마나 가까운지와 추정치의 불확실성을 모두 고려
      • 실제로 최적일 가능성에 따라 탐욕스럽지 않은 action 을 선택하는 것이 좋음.

      2_7_1_UCB

      • UCB (Upper-Confidence-Bound) Action Selection 은 그러한 효율적인 방식 중 하나이다.
      • $N_t(a)$ 는 t step 이 진행되었을때 a action 이 선택된 횟수로, 많이 선택될 수록 우항의 피연산자 값이 작아진다.
      • $\ln t$ 는 step 이 커짐에 따라 값이 무한대까지 증가 (수렴하지 않음) 하나 그 증가폭이 서서히 줄어든다
      • $c$ 는 탐험의 정도 (강도) 를 나타내는 수치이다.
      • 즉 action이 많이 선택될수록 $Q_t(a)$ 의 값은 정확해지고, 우항의 피연산자 값은 작아진다.
      • action 이 한번도 선택되지 않을 경우 해당 a 를 maximizing action 으로 여긴다. (해당 a 에 대한 무조건적인 탐험)

      2_7_2_UCB

      • 이러한 UCB 방식은 10-armed testbed 에서 $\varepsilon$-greedy 보다 나은 성과를 보여주기도 한다.
      • 단 몇가지 단점으로 인해 실용적이지 않은 방식이다.
        • bandits 문제에서 reinforcement learning 문제로 확장하기 어렵다.
        • nonstationary 한 문제들에는 더 어려운 방식의 action-value method 가 필요하다.
        • 훨신 더 거대한 환경 (state space) 에서의 적용 (특히 뒤에 배울 function approximation 방식) 이 어렵다.

Lesson 1: The K-Armed Bandit Problem

  • 학습목표
    • Define reward
    • Understand the temporal nature of the bandit problem
    • Define k-armed bandit
    • Define action-values
  • Sequential Decision Making with Evaluative Feedback
    • 불확실성 아래에서의 의사결정
      • 의사가 3가지 처방약으로 환자에게 실험적 처방을 할 때…
      • 몇번의 환자 반응을 보고 가장 잘 듣는 약을 고집할 경우
        • 더이상 다른 약의 데이터를 모을 수 없음
        • 나머지 두 약이 실제로 나음에도 몇몇 결과가 나쁘게 나왔는지 알 수 없음
      • 다른 약으로 계속 실험할 경우
        • 나쁜 결과를 계속 초래할 수 있음
    • 강화학습에서의 기초적 컨셉 용어
      • 에이전트 (Agent) : action을 선택하는 존재 - 의사
      • 액션 (Action) : 선택지 - 3가지 약 중 하나를 선택하는 것
      • 보상 (Rewards) : 액션에 대한 결과 - 환자의 상태
      • 값 (Value Function - Action-Value (Function)) : 기대되는 보상 값 - 환자의 혈압 값
        • 에이전트가 액션을 선택했을 때 그 값 (Action-Value = $q_*$)이 최대화 할 경우 목적을 달성함
    • $q_*(a)$ 값 구하기
      • 각 약의 결과값이 서로 다른 확률분포를 가졌을 경우 $q_*$ 는 각 분포의 평균이 될 수 있다.
    • Bandits Problem 을 고려하는 이유
      • 문제와 알고리즘 디자인 선택에 있어 가장 간단한 세팅

Lesson 2: What to Learn? Estimating Action Values

  • 학습목표
    • Define action-value estimation methods
    • Define exploration and exploitation
    • Select actions greedily using an action-value function
    • Define online learning
    • Understand a simple online sample-average action-value estimation method
    • Define the general online update equation
    • Understand why we might use a constant step-size in the case of non-stationarity
  • Learning Action Values
    • Estimate action values using the sample-average method
      • 의사가 처방 후 환자가 나아질 경우 1, 그렇지 않은 경우 0 으로 표기하고 3개의 약을 처방해 평균을 구함
      • Step 이 많이 진행될 수록 평균 데이터는 더 정확해짐
    • Describe greedy action selection
      • 의시가 해당 시점에 가장 기대치가 큰 약을 처방할 경우 이 행동을 Greedy action 이라고 함
      • greedy action 을 선택하는 것을 현 지식을 활용한 이용 (exploitation) 이라고 함
      • 당장의 기대되는 보상을 포기하고 다른 선택을 하는 것을 non-greedy action 이라고 하고 이를 탐험 (exploration) 이라고 함
      • 탐험을 통해 기대되는 보상을 희생하고 non-greedy action 의 보상에 대한 더 많은 정보를 얻게 됨
    • Introduce the exploration-exploitation dilemma
      • 에이전트는 동시에 탐험과 이용을 할 수 없음
  • Estimating Action Values Incrementally
    • action value 의 점진적 표현법 (sample-average method 를 이용)
      • Incremental update rule
      • NewEstimate <- OldEstimate + StepSize(Target - OldEstimate)
    • 점진적 업데이트 룰(Incremental update rule)이 더 널리 쓰이는 이유
      • 모든 이전 값들을 기억할 필요가 없다.
    • 보편적 업데이트 룰을 non-stationary bandit problem 에 적용하는 방법
      • Non-stationary Bandit Problem : 의사의 3가지 약중 특정 하나의 약이 겨울이 되면 효율이 높아진다.
      • 보상의 분포가 시간에 따라 변하게 되는 경우를 Non-stationary 하다 라고 함.
      • StepSize 파라미터가 상수 (예:0.1) 일 경우 이전 Step 일수록 영향도가 작아지고, 최신 Step의 보상값을 더 반영함.

Lesson 3: Exploration vs. Exploitation Tradeoff

  • 학습목표
    • Define epsilon-greedy
    • Compare the short-term benefits of exploitation and the long-term benefits of exploration
    • Understand optimistic initial values
    • Describe the benefits of optimistic initial values for early exploration
    • Explain the criticisms of optimistic initial values
    • Describe the upper confidence bound action selection method
    • Define optimism in the face of uncertainty
  • What is the trade-off?
    • exploration-exploitation 의 등가교환
      • Exploration (탐색) : 장기적 이익을 위해 지식을 늘림
      • Exploitation (이용) : 단기적 이익을 위해 지식을 이용
      • 탐색만 하면 단기적 보상이 작아지고, 이용만 하면 타 선택지의 true value 를 모르기 때문에 장기적으로 손해일 수 있음
      • 한번의 선택에서 탐색 과 이용 둘 중 하나만 가능
    • Epsilon-Greedy 방식 (탐색과 이용의 균형을 맞추는 쉬운 방법)
      • Epsilon-Greedy 는 대부분 Exploitation (Greedy method) 하고, 적은 확률로 Exploration (Random choice) 한다.
    • 각 방식을 비교할 때 한 번의 진행으로는 노이즈가 많아 확인이 어려움.
      • 1000 개의 에이전트로 보상 데이터를 모아 평균값으로 비교
  • Optimistic Initial Values
    • Optimistic initial values 가 초기 탐색을 장려하는 이유
      • 초기 예상 보상치를 높게 잡고 시작
      • 첫 선택의 보상이 주어지더라도 평균값으로 인해 값이 떨어짐
      • 에이전트는 첫 선택에 실망을 하고 선택되지 않은 다른 높은 초기치의 옵션 중 하나를 선택
      • 초기 탐험을 통해 모든 Action 을 골고루 선택하게 됨.
    • Optimistic initial values 의 한계
      • 초기 단계에서만 탐색을 진행한다. 이는 Non-stationary Problems 에서 문제가 됨.
      • Maximal Reward 를 시작하기 전 알 방법이 없기에 Optimistic Initial Value 를 어느정도로 설정해야 할지 모른다.
      • 그럼에도 Optimistic initial values 는 휴리스틱 (충분한 정보 없이 빠르게 사용할 수 있는 직관적인) 한 방법으로 자주 활용됨
  • Upper-Confidence Bound(UCB) Action Selection
    • UCB action-selection 방식이 예측의 불확실성을 이용해 탐색을 유도하는 방법
    • UCB의 C는 confidence 를 뜻하며, 예측한 $Q(a)$ 값의 오차범주 범위 $(c)$ 내에 실제 값이 들어올 것이라 확신하는 정도의 수치이다.
      • 범위가 작을수록 결과에 더욱 확신한다는 뜻임
    • 불확실성 (범위) 에 마주했을때 가장 높은 값 (Upper-Confidence Bound) 을 선택
    • 수식에 대한 풀이
      • c : 사용자 정의 파라미터 (얼마나 탐험을 할 건지 컨트롤)
      • 좌측 피연산자 : Exploit (이용)
      • 우측 피연산자 : Explore (탐험)
  • Contextual Bandits for Real World Reinforcement Learning
    • Contextual Bandits 는 Reinforcement Learning 이 현실에 배포되는 방식임
    • Reinforcement 는 현실과 어떻게 다른가?
      • Reinforcement Learning 은 시뮬레이터로 동작한다.
        • 시뮬레이터는 관측치를 제공
        • Learning 알고리즘은 어떤 Action을 선택할 지 정책을 가진다.
        • 시뮬레이터는 실행하고 보상을 제공한다.
      • 현실이 제공하는 관측값은 시뮬레이터와 다르다.
        • 같은 정책이라 해도 관측치가 다르기 때문에 시뮬레이터에서의 Action 과 다른 Action 을 수행하게 된다.
        • 시뮬레이터와 현실은 보상도 다르다.
      • 즉 현실과 시뮬레이터에는 갭이 존재한다.
    • Real World based Reinforcement Learning : 현실 기반 강화학습을 하려면 우선순위를 변경해야 함
      • Temporal Credit Assignment < Generalization
        • Temporal Credit Assignment Problem (CAP) : 시간적 기여도 할당문제. 일련의 행동이 모두 끝난 뒤 보상을 얻을 수 있는 환경에서 수행한 행동들 중 어떠한 행동이 기여도가 있고 어떠한 행동이 벌점을 줄 것인지 결정하는 문제.
        • Generalization : 다양한 관찰값을 통한 일반화
      • Control environment < Environment controls
        • 시뮬레이션 환경에서는 자유자재로 한 스텝을 더 진행하거나 할 수 있다면 (컨트롤 가능)
        • 현실에서는 환경이 지배함. (환경에 의해 컨트롤당함)
      • Computational efficiency < Statistical efficiency
        • 시뮬레이션 환경에서 계산효율이 중요하다면 (학습할 샘플이 많으므로)
        • 현실에서는 통계적 효율이 중요함 (현실이 주는 샘플만 가질 수 있다.)
      • State < Features
        • 시뮬레이션에서는 상태를 생각 (상태값은 결정을 내리는 데 기반이 되는 요소)
        • 현실에서는 매우 복잡한 관측값을 가지는 경우 (필요한 것보다 정보가 많음) 가 많아 어느 것이 핵심 요인인지가 중요
      • Learning < Evaluation
        • 현실에서는 “Off Policy Evaluation” 이 중요하다.
          • Off Policy : 정책 업데이트에 어떤 데이터를 써도 상관이 없는 경우
          • 즉, 최신 업데이트 정책에서 수집된 데이터가 아니어도 사용가능
          • 학습 알고리즘이 학습 뿐만 아니라 정책 평가에 쓰일 수 있는 부산물 데이터 또한 제공
      • Last policy < Every Policy
        • 시뮬레이션에서는 가장 최신의 정책이 중요
        • 현실에서는 모든 포인트의 데이터가 세상과의 어느 정도 상호작용이 포함되어 있음

Chapter Summary (RLbook2018 Pages 42-43)

Weekly Assessment

댓글남기기

참고