HY03

HY03

저는 전문가가 아니고 이것 저것 알아보는 비전문가 입니다.
틀린 내용이 기술되어도 너그러이 봐주시고 댓글을 남겨주셨으면 좋겠습니다.

Prediction and Control with Function Approximation - 03. Week 3. Control with Approximation

관련 자료 (RLbook Pages 243-246, 249-252)

Chap.10 On-policy Control with Approximation

  • 이번 챕터에서는 제어 문제에 대해 집중한다.
    • action-value function 의 근사화 함수 $\hat{q} (s,a, \textbf{w} ) \approx q_*(s,a)$
    • $\textbf{w} \in \mathbb{R}^d$ (유한 차원의 가중치 벡터)
    • 이번 쳅터에서는 on-policy 의 경우에 집중한다. (off-policy 는 11장에서 다룬다.)
  • 이 장에서는 semi-gradient Sarsa 알고리즘에 대해 다룬다.
    • semi-gradient TD(0) 를 action value 와 on-policy control 로 자연스럽게 확장한다.
    • episodic case 에서는 이 확장이 직관적이나, continuing case 에서는 최적 정책을 정의하기 위한 할인에 대한 개념을 고려해야 한다.
    • 놀랍게도 우리가 참 함수근사를 가지게 된다면, 할인을 포기하고 새로운 “average-reward” 공식을 새로운 “differential” value function 에 적용해야 한다.

10.1 Episodic Semi-gradient Control

  • semi-gradient prediction methods 를 action values 로 확장하는 것은 직관적이다.
    • action-value function 의 근사화, $\hat{q} \approx q_\pi$ 를 가중치 벡터 $\textbf{w}$ 로 파라미터화된 함수화 형태를 만드는 것.
    • 이전에 고려하였던 $S_t \mapsto U_t$ 에 대해 이제는 $S_t, A_t \mapsto U_t$ 를 고려한다.
    • 업데이트 타겟 $U_t$ 는 $q_\pi (S_t,A_t)$ 의 어떠한 근사치도 될 수 있다.
    • 가령 통상적인 backed-up value 들, full Monte Carlo return ($G_t$) 또는 n-step Sarsa returns 가 될 수 있다.

  • 보편적인 gradient-descent update for action-value prediction

    10_1_1_gradient_descent_update_for_action_value_prediction

  • episodic semi-gradient one-step Sarsa

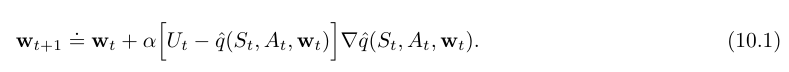
    10_1_2_episodic_semi_gradient_one_step_sarsa

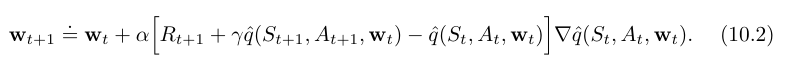
    • 이 방식 또한 TD(0) 와 같은 방식으로 수렴하고, 같은 error 범위를 가지게 된다. (단 가치함수근사가 선형임을 전제로 함.)
  • control methods
    • 우리는 action-value prediction methods 와 쌍을 이루는 policy improvement 와 action selection 기술이 필요하다.
    • 이산적이지 않은 연속적인 actions 와 거대한 이산 action sets 환경에서의 기술은 아직 논의 중이다.
    • 반면 action 이 이산적이고 크지 않은 집합이라면 이미 개발된 기술들을 사용할 수 있다.
    • 가령 현 상태 $S_t$ 에서 각각의 가능한 행동 $a$ 가 있다면 우리는 $\hat{q} (S_t, a, \textbf{w}_t )$ 를 계산해 낼 수 있고
    • greedy action $A^*_t = \arg\max_a \hat{q}(S_t,a, \textbf{w}_t)$ 를 찾을 수 있다.
    • 정책 개선은 이 예측 정책을 탐욕 정책의 soft approximation (예를 들어 $\epsilon$-greedy policy) 로 변경하는 것으로 끝나며, 행동 또한 동일 정책으로 선택되면 된다.

    10_1_3_episodic_semi_gradient_sarsa_pseudo_code

10.3 Average Reward: A New Problem Setting for Continuing Tasks

  • average reward settings
    • Markov decision problems (MDPs) 에서 에피소드와 할인 설정 외의 고전적인 세팅 방법
    • continuing problems - 종료 혹은 시작상태 없이 환경과 에이전트가 계속 상호작용 하는 문제 에 적용된다.
    • 할인이 없이 에이전트는 지연된 보상을 즉각적인 보상과 같이 생각한다.
    • dynamic programming 에서는 고전적인 이론으로 여겨지고, 강화학습에서는 덜 사용한다.
    • 다음 섹션에서 우리는 discounted setting 이 근사 함수와 문제가 있고, 그렇기에 average-reward setting 이 그것을 대체함을 논의할 것이다.

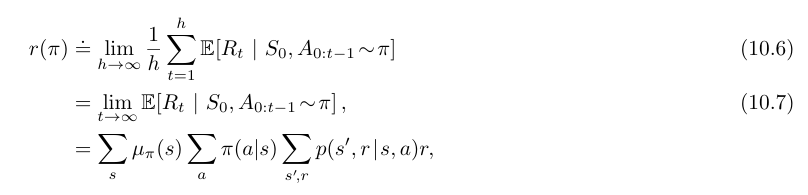
    10_3_1_average_reward_settings

    • average-reward setting 에서 정책 $\pi$ 은 보상의 평균으로 평가되며, 이것을 $r(\pi)$ 로 표기한다.
  • Ergodicity (에르고딕성)
    • 기대값은 초기 상태 $S_0$ 와 이후의 행동 $A_0,A_1,…,A_{t-1}$ 가 정책 $\pi$ 에 따라 선택된다는 조건 하에 계산된다.
    • $\mu_\pi$ 는 안정 상태 분포 (steady-state distribution) 으로 정의되며, 다음과 같이 나타낼 수 있다.
    • $\mu_\pi(s) \doteq \lim_{t \to \infty} Pr [ S_t=s | A_{0:t-1} \sim \pi ]$
    • 이는 주어진 $\pi$ 에 대해 항상 존재하며 초기 상태 $S_0$ 에 독립적이라고 가정한다.
    • MDP 에 대한 이러한 가정을 에르고딕성 (ergodicity) 라 한다.
    • 이는 MDP 가 어디에서 시작하든지 또는 에이전트가 초기에 어느 결정을 내리든지 간에, 이러한 결정들은 일시적 효과만을 가질수 있다는 것을 의미한다.
    • 장기적으로 한 상태에 있을 확률의 기대값은 오직 정책과 MDP 의 전이 확률에 의존하게 된다.
    • 그렇기에 위의 수식이 안정적으로 수렴함을 보장할 수 있다.
  • 평균 보상 접근법을 통한 정책의 최적성 평가
    • 할인되지 않은 지속적인 경우에서 최적성의 종류 간에는 미묘한 차이점이 있다.
    • 그러나 대부분의 실용적인 목적을 위해서는 정책들을 시간 단계당 평균 보상, 즉 $r(\pi)$ 에 따라 순서를 매기는 것만으로도 충분할 수 있다.
    • 이는 정책 $\pi$ 하의 평균 보상으로 다음과 같이 제안된다.
      • $\lim_{t \to \infty} \mathbb{E} [ R_t | S_0, A_{0:t-1} \sim \pi ]$
    • 특히, $r(\pi)$ 의 최대 값을 달성하는 모든 정책을 최적이라고 간주한다.
  • Average-reward setting 에서 안정적 상태 분포와 차분 가치 함수
    • 안정적 상태 분포 (steady state distribution) : 정책 $\pi$ 를 따라 행동을 선택하였을 때, 같은 분포가 되는 상태

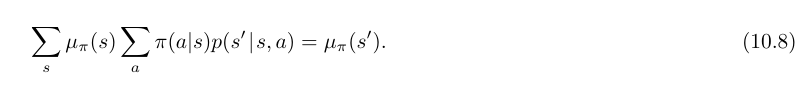
    10_3_2_steady_state_distribution

    • average-reward setting 에서 보상값은 보상과 평균 보상의 차로 정의된다.

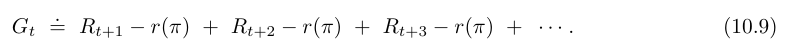
    10_3_3_differential_return

    • 이는 differential return (차분 보상) 이라 하고, 이에 상응하는 가치 함수는 differential value function (차분 가치 함수) 라 한다.
    • 같은 방식의 표현을 사용한다.
      • $v_\pi(s) \doteq \mathbb{E}_\pi [G_t | S_t=s]$
      • $q_\pi (s,a) \doteq \mathbb{E}_\pi [G_t | S_t=s, A_t=a]$
    • Differential value function 또한 Bellman equations 를 가지고 있다.
    • 이는 간단히 $\gamma$ 를 제거하고, 보상 대신 보상과 true average reward 의 차를 사용하는 차이점이 있다.

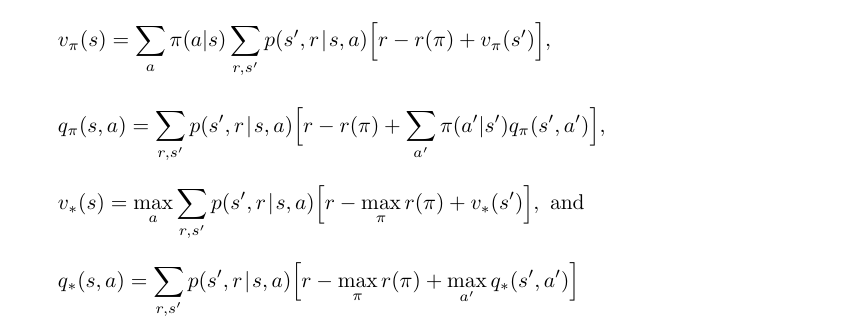
    10_3_4_differential_value_function_bellman_equations

    • 또한 TD error 에 대한 differential form 도 있다.

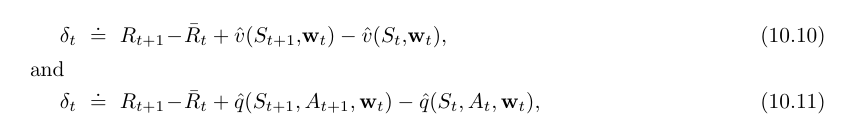
    10_3_5_differential_form_td_error

    • $\bar{R}_t$ : 시간 t 에서의 평균 보상 $r(\pi)$ 의 추정치
    • 이러한 변형된 정의에서 평균보상 세팅을 통한 대부분의 알고리즘과 많은 이론적 결과는 변화 없이 적용이 된다.
    • 예를 들어 semi-gradient Sarsa 의 average reward 버전은. 위의 변형된 TD error 를 사용한다.

    10_3_6_semi_gradient_sarsa_average_reward_version

    • 이에 대한 pseudo code 는 아래와 같다.

    10_3_7_semi_gradient_sarsa_pseudo_code

Episodic Sarsa with Function Approximation

Episodic Sarsa with Function Approximation

  • 학습목표
    • 어떻게 행동-가치 근사를 위해 행동 종속적인 feature 를 구성하는지 이해
    • 어떻게 episodic tasks 에서 함수 근사를 이용한 Sarsa 를 적용하는지 이해

  • State-values to action-values

    episodic_sarsa_with_function_approximation_state_values_to_action_values

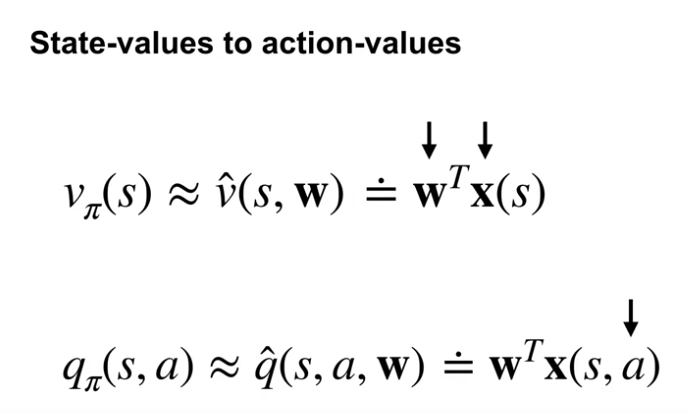
    • value function approximation 은 weight vector 와 feature vector, 2개의 구성요소를 가지고 있다.
    • State-value function approximation 에서는 주어진 상태에 대해 이 2개의 요소의 내적 연산을 통해 가치 추정을 한다.
    • TD 에서 Sarsa 로 전환하기 위해 우리는 action value function 을 사용해야 한다.
    • 따라서 feature 의 표현에서 action 또한 표현이 되어야 한다.

  • Representing actions

    episodic_sarsa_with_function_approximation_representing_actions

    • feature 의 표현에 action 이 포함되는 하나의 방법으로 각 행동에 대응하도록 function approximator 를 분리하는 것이다.
      • stacking the features
      • 즉, 각각의 행동에 대해 같은 상태 feature 를 사용하며, 단 해당하는 행동에 대응하는 feature 만 활성화 하는 것

  • Computing action-values

    episodic_sarsa_with_function_approximation_computing_action_values

    • 4개의 요소를 가진 상태 feature 와 3개의 action 이 있다고 가정
    • action 에 해당하는 상태 feature 만 활성화
    • stacking features : 상태와 행동을 함께 포함하는 특성을 표현하는 방식
  • Computing Action-values with a Neural Network
    • 위의 Stacking feature 방식으로 action value 를 계산하는 것이 선형 함수 근사에 특화된 것으로 생각할 수 있으나 그렇지 않다.
    • 신경망의 경우
      • 상태를 입력으로 받음
      • 마지막 은닉층에서 상태 특성을 생성
      • 위 상태 특성에 각 행동 가치에 해당하는 별개의 가중치를 연산, 별도의 출력을 생성
      • 한 행동 가치의 가중치는 다른 행동 가치의 가중치와 상호작용하지 않음 (Stacking 과 동일)
    • 즉 신경망에서 각 행동 가치가 독립적인 가중치 집합으로 계산되는 방식이 Stacking 과 동일한 개념이다.
    • 둘 다 행동 가치를 독립적으로 계산하기 때문에 한 행동 가치의 가중치는 다른 행동 가치에 영향을 미치지 않는다.
    • 단 상태와 마찬가지로 행동 또한 일반화시키고 싶은 경우 행동 또한 상태와 포함하여 feature 로 구성해야 한다.

  • Episodic Sarsa with function approximation

    10_1_3_episodic_semi_gradient_sarsa_pseudo_code

Episodic Sarsa in Mountain Car

  • 학습목표
    • approximate TD control method 의 성능 분석에 대한 경험

  • The Mountain Car environment

    episodic_sarsa_in_mountain_car_the_mountain_car_environment

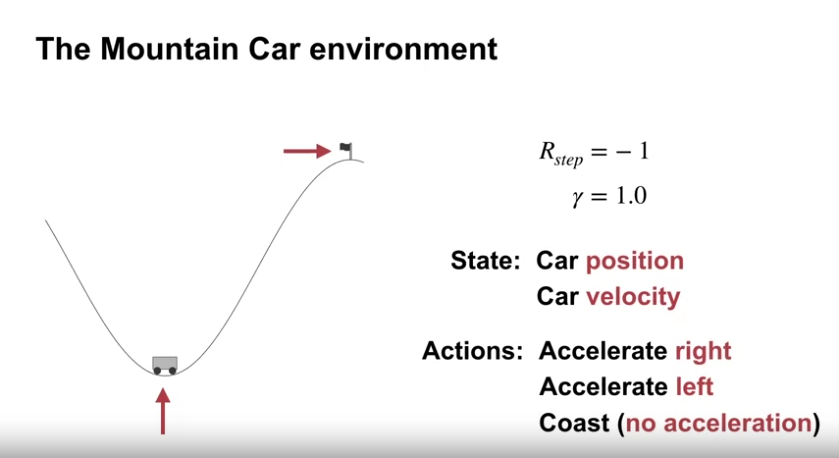
    • episodic task
    • 목표 : 동력이 부족한 (중력이 자동차의 엔진보다 강함) 자동차를 산의 우측 경사 위의 목적지에 도달하게 만드는 것
      • 자동차가 바로 올라갈 수 없고, 반대방향 등으로 이동하여 모멘텀을 얻어 목적지에 도달하여야 함.
    • 초기 상태 : 계곡 밑바닥의 근처 랜덤한 장소에서 시작
    • 종료 상태 : 언덕 꼭대기위 깃발 위치에 도달
    • 빠른 시간 내에 목표 달성을 위해 각 시간 스텝마다 보상 수치에 -1을 적용
    • 할인 : 없음
    • 상태값 : 자동차의 위치, 자동차의 속도 (2차원 연속 공간)
    • 행동값 : 전진, 후진, 가속없음

  • Feature representation

    episodic_sarsa_in_mountain_car_feature_representation

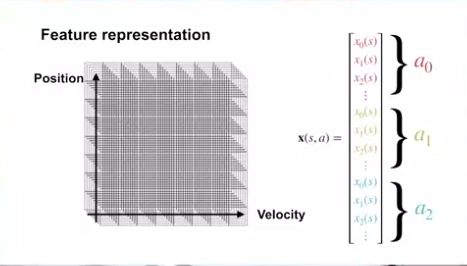
    • feature 는 위치와 속도로 이루어짐
    • tile coding 기법을 사용하며, 8x8 그리드(타일)을 8 타일링 사용
    • action 은 개별적으로 다루며, stacked feature 표현법을 사용한다.
    • 보상 초기 값은 0으로 세팅 (이는 매우 긍정적인 세팅으로, 실제 보상값이 -1씩 줄기 때문에 보상이 0보다 커질 수 없음)
      • 위의 세팅으로 시스템적인 탐험을 일으킴
      • 위의 세팅으로 타 탐험정책 없이 그리드 정책을 운영할 수 있음

  • Learned values

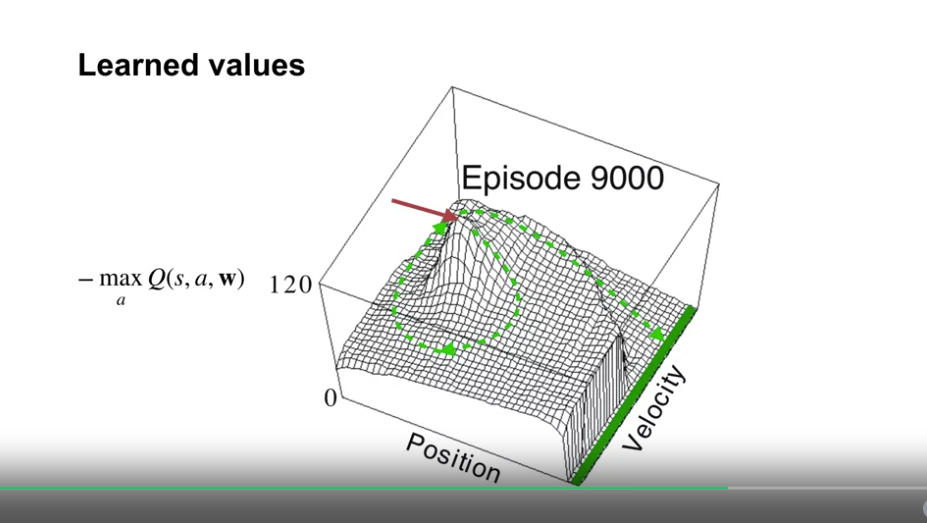
    episodic_sarsa_in_mountain_car_learned_values_1

    • 상태의 값을 샘플링하여 시각화함 (상태의 값이 연속적이어서, 모든 상태의 탐험이 불가능함)
    • $- \max_a Q(s,a, \textbf{w})$ 수치 사용 : step 마다 -1 의 보상이 적용되는데, 이 값으로 몇 스텝 후에 종료될지를 예상함
    • 화살표 포인트가 시작점이며, 초록색 점선이 최적의 trajetory 를 가리킨다.

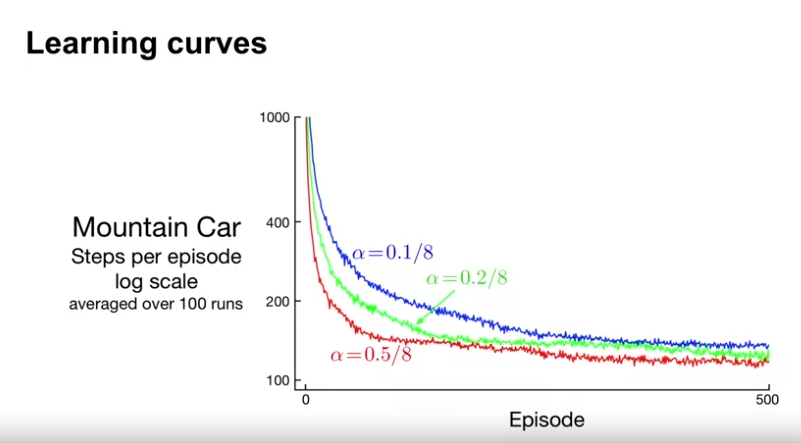
    episodic_sarsa_in_mountain_car_learning_curve

    • learning curve 는 학습의 속도에 더 나은 insight 를 제공한다.
    • $\alpha$ (step size) 값이 작을수록 학습 속도가 느렸음
    • 모든 $\alpha$ 값이 8로 나누어짐
      • step size vector 를 사용하지 않을 경우 보편적으로 feature vector의 norm (길이) 값을 사용
      • 여기서는 8개의 타일링을 사용하였으므로, 1의 feature vector 의 길이는 8이 된다.
    • 위의 부연설명 (Chat-GPT)
      • tiling 한 숫자만큼 하나의 상태가 여러 타일에 속하게 되고, 여러 가중치가 업데이트되어 이것이 과도한 영향을 주는 요인이 될 수 있다.
      • tiling 의 수만큼 나누어줌으로서, 학습과정의 안정성을 높이게 된다. (normalization)

Expected Sarsa with Function Approximation

  • 학습목표
    • 함수 근사를 이용한 Expected Sarsa 업데이트에 대해 설명하기
    • 함수 근사를 이용한 Q-learning 에 대해 설명하기

  • From Sarsa to Expected Sarsa

    expected_sarsa_with_function_approximation_from_sarsa_to_expected_sarsa

    • Sarsa : 업데이트 할 때 다음 상태와 행동을 선택하여 업데이트한다. (On-policy)
    • Expected Sarsa : 정책에 따른 다음 상태의 모든 행동예측값을 이용해 업데이트한다. (Off-policy)
    • On-policy
      • 장점 : 정책 일관성, 안정성, 탐험-이용 균형 유지
      • 단점 : 학습 효율성 낮음, 로컬최적화 위험
    • Off-policy
      • 장점 : 학습 효율성 높음, 데이터 재사용 가능, 전역 최적화 탐색 가능
      • 단점 : 불안정성, 수렴 문제, 정책 일관성 부족

  • Expected Sarsa with Function Approximation

    expected_sarsa_with_function_approximation_expected_sarsa_with_function_approximation

    • 위의 식과 같이 $\textbf{w}$ 를 TD error 값을 이용해 업데이트 해 나아간다.

  • Expected Sarsa to Q-learning

    expected_sarsa_with_function_approximation_expected_sarsa_to_q_learning

    • Q-learning 은 Expected-Sarsa 의 특이 케이스 중 하나이다. (학습하려는 정책이 Greedy policy 인 Expected Sarsa)

Exploration under Function Approximation

Exploration under Function Approximation

  • 학습목표
    • 함수 근사에서의 낙관적 초기값을 통한 탐색-이용과 $\epsilon$-greedy 방식을 통한 탐색-이용 방식에 대한 설명

  • Optimitic Initial Values in the Tabular Setting

    exploration_under_function_approximation_optimistic_initial_values_in_the_tabular_setting

    • agent 가 실제 보상값보다 더 큰 보상값을 얻을 것이라고 상상하는 것
    • 이는 에이전트로 하여금 상태-행동 공간에서 시스템적인 탐색을 유도한다.
    • 이는 Tabular Setting 에서 하나의 상태-행동 쌍이 다른 상태-행동 쌍의 값에 영향을 미치지 않기에 가능하다.

  • How to Initialize Values Optimistically under Function Approximation

    exploration_under_function_approximation_how_to_initiallize_values_optimistically_under_function_approximation

    • 함수 근사에서 낙관적인 초기값을 세팅한다는 것은, 낙관적 결과값을 위해 가중치 벡터를 세팅한다는 것과 같은 의미이다.
      • 이는 특수한 환경에서는 쉽게 가능한데, 이를테면 binary feature 일 경우이다.
      • binary feature : 모든 상태-행동 쌍에 대응하는 하나의 가중치가 존재하며, feature 값은 1과 0으로 표현됨.
    • 대부분의 문제에서는 낙관적인 초기값을 세팅하는 것이 불가능하다.
      • 신경망에서는 가중치를 조절하여 낙관적인 결과값을 유도하는 것은 꽤 복잡한 문제이다.
      • 예를 들어 tanh 활성화 함수를 사용할 경우 초기 가중치가 양수여도 음수의 결과값이 나올 수도 있다.

  • How Optimism Interacts with Generalization

    exploration_under_function_approximation_how_optimism_interacts_with_generalization

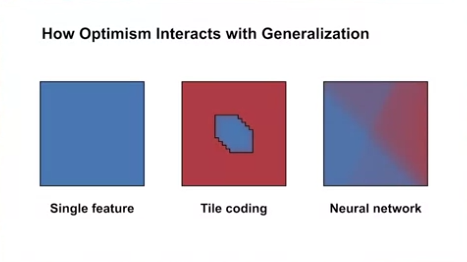
    • 어떻게 feature 값을 일반화하였느냐에 따라, 낙관적 초기값은 tabular case 와 같은 시스템적 탐색을 하지 못할 수도 있다.
      • 방문하지 않은 영향을 받는 상태까지도 다 같이 업데이트가 됨.

  • $\epsilon$-greedy

    exploration_under_function_approximation_epsilon_greedy

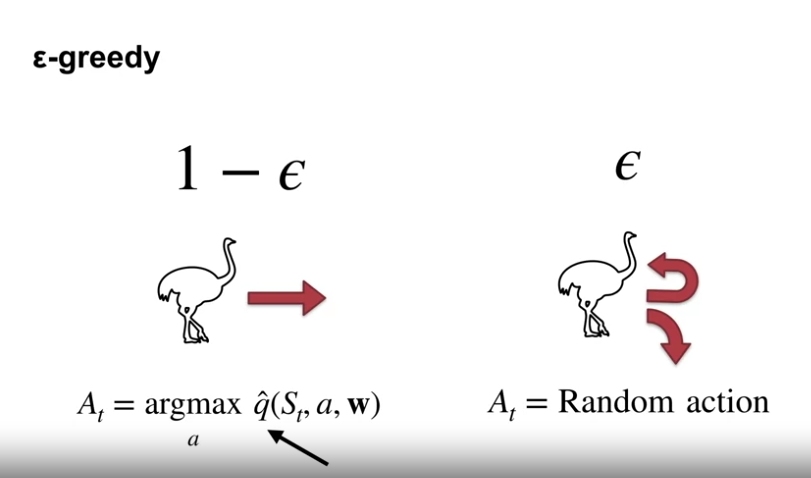
    • $\epsilon$-greedy 는 광범위하게 사용되며, Non-linear 함수 근사에서도 쉽게 사용될 수 있다.
    • 어떻게 초기화되고 근사화되었냐에 무관하게 행동 가치 추정만 필요하다.
    • 그러나 $\epsilon$-greedy 는 직접적인 탐험 방법이 아니며, 해당 상태에서 할 수 있는 행동에 대한 랜덤한 확률에 의존하여 더 나은 정책을 찾는 방법이다.
      • 낙관성에 의존한 시스템 적인 탐색방법이 아니다.
    • 함수 근사에서 탐색방법의 발전은 아직 열린 질문이며 이 과정에서는 이 심플한 방법에 의존한다.

Average Reward

Average Reward : A New Way of Formulating Control Problems

  • 개요
    • Continuing tasks 에서 우리는 엄청나게 긴 흐름의 성능에 관심이 있을 수 있다.
    • 지금까지 우리는 discounting 을 사용해 단기 성과와 장기 이익의 균형을 맞춰왔다.
    • 위의 방식과 다른 average reward 공식을 이용한 방법에 대해 살펴본다.
  • 학습목표
    • average reward setting 에 대해 서술
    • Average reward optimal policies 와 discounting 을 통해 얻은 policies 간의 차이에 대한 설명
    • 차분 가치 함수의 이해

  • A simple example

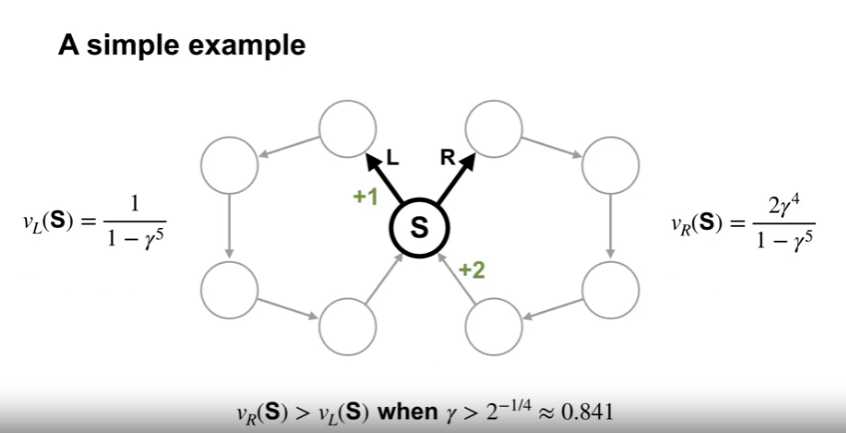
    average_reward_a_simple_example

    • 근시안적인 MDP 문제 (Continuing tasks)
    • 대부분의 상태에서는 하나의 행동만이 존재하여 결정할 것이 없고, 오직 하나의 상태 (교차점) 에서만 정책 결정이 이루어진다.
      • 이 지점에서 어떠한 ring 으로 순환할 지 결정할 수 있다. (두 개의 결정론적인 정책이 존재)
    • 위의 표기된 보상 외에 타 전이에서의 보상은 0이다.
    • Discounting 을 사용하는 경우
      • $\gamma$ = 0.5
        • $v_L (S) \approx 1$
        • $v_R (S) \approx 0.1$
      • $\gamma$ = 0.9
        • $v_L (S) \approx 2.4$
        • $v_R (S) \approx 3.2$
      • 즉, 할인율 (0.841) 과 상태의 수 (100개의 상태일 경우 0.99)에 따라 최적 정책이 달라지게 된다.
      • continuing task 에서 할인율을 1로 하였을 경우 반환값이 무한대가 될 수 있다.
      • 할인율 값이 크면, 더해야 할 변수가 늘어 학습이 어렵게 된다.

  • The Average Reward objective

    average_reward_the_average_reward_objective

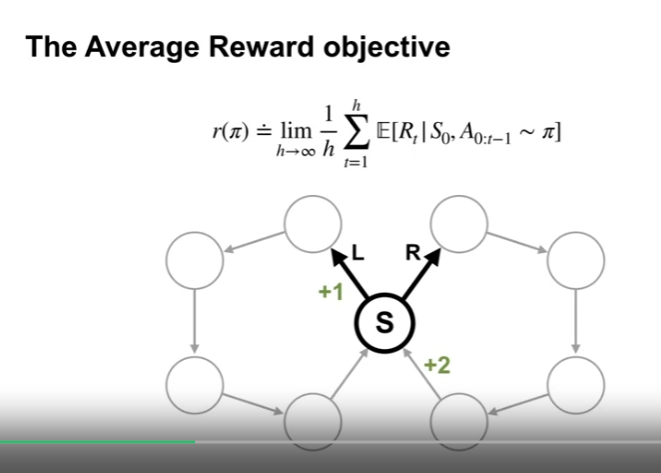
    • 하나의 정책에서 위의 average reward 를 최대화 하는 목표는 장단기 보상을 동일하게 생각한다는 의미이다.
      • 위의 값을 $r(\pi)$ 로 표현한다.

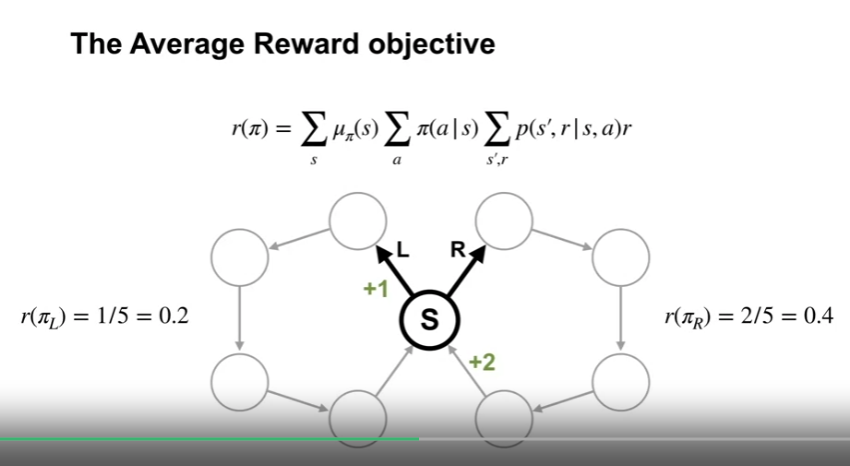
    average_reward_the_average_reward_objective_mu

    • 또한 특정 상태에 있을 확률값을 나타내는 $\mu$ 를 이용하여 식을 위와같이 변형할 수 있다.
  • Returns for Average Reward
    • average reward 정의는 어떤 정책이 더 나은지에 대해 직관적으로 표현된다.
    • 그렇다면 우리는 어떻게 특정 상태의 행동이 더 나은 것인지 판단할 수 있을까?
      • 즉 행동가치가 필요함
    • average reward setting 에서 리턴값은 보상값과 average reward $r(\pi)$ 의 차로 정의된다.

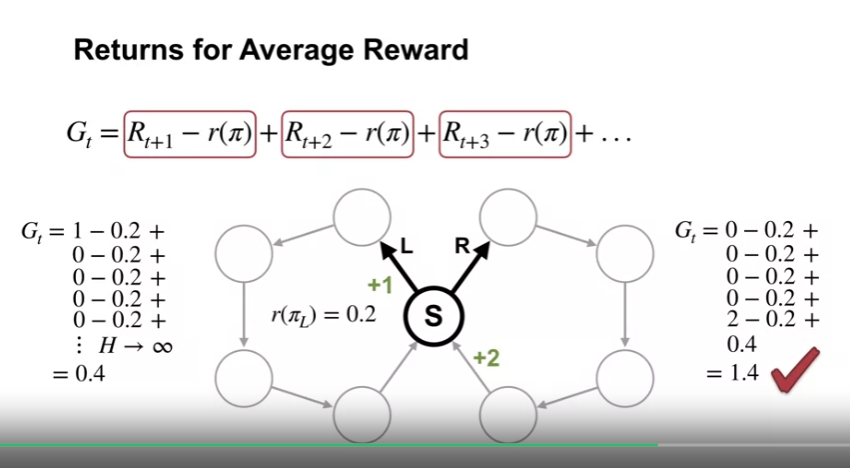
    average_reward_returns_for_average_reward_1

    • 좌측으로 도는 정책의 Cesaro Sum 을 이용하여 average reward setting 의 리턴값을 계산해보면 0.4가 된다.
      • n-1 바퀴까지 0으로 상쇄, n 번째에서 누적합의 평균을 구함
    • 이를 이용해 우측 한바퀴를 돈뒤 좌측으로 도는 정책을 생각해보면 값은 1.4가 되고, 우측으로 도는 행동이 더 나은 행동임을 알 수 있다.

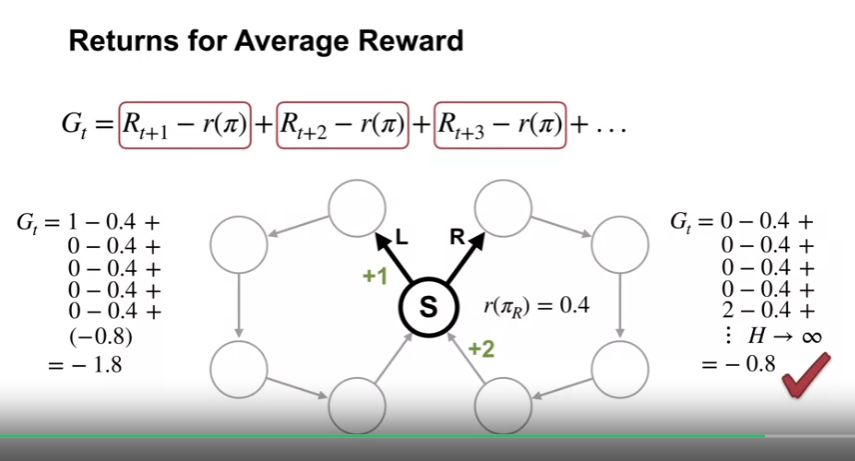
    average_reward_returns_for_average_reward_2

    • 오른쪽으로 도는 정책을 기준으로 왼쪽으로 도는 정책과 비교한 경우
    • 차등 수익 (differential return) 은 후속 시간 단계에서 동일한 정책을 따르는 경우에만 행동에 대해 비교할 수 있다.
    • 정책을 비교할 경우 average reward 값을 비교한다.
    • 차등 수익의 경우 차감된 상수가 실제 평균 보상과 동일한 경우에만 수렴하고 그외의 경우 양수 또는 음수 무한대로 발산한다.

  • Value Functions for Average Reward

    average_reward_value_functions_for_average_reward

    • 위와 같이 Average reward 에 대한 리턴값이 정의됨.
    • 가치함수는 일반적인 방식대로 예상 리턴값으로 정의할 수 있음
    • 이 값은 에이전트가 고정된 정책을 따랐을 때 모든 상태에 대한 평균 보상값이 아닌 특정상태에서 행동함으로써 에이전트가 얼마나 더 많은 보상을 얻는지를 시사함
    • discount 세팅처럼 average reward 또한 bellman 방정식에 사용할 수 있으며, 다른 점은 즉각적 보상에서 $r(\pi)$ 를 차감한다는 점과 discount 가 없다는 점이다.

  • Differential Sarsa

    differential_sarsa_differential_semi_gradient_sarsa_for_estimating

Satinder Singh - On the Optimal Reward Problem (Where do Rewards Come From?)

  • 보상함수의 출처
    • 일반적인 강화학습은 보상이 환경으로부터 주어지는 것으로 가정
    • 하지만 실제로 이 보상은 설계자가 정하는 것 (설계자가 에이전트의 행동에 대한 선호도를 반영)
    • 보상함수는 에이전트 설계자의 선호도를 반영하는 동시에 에이전트의 목표나 목적을 설정하는 매개변수 역할을 함
    • 따라서 설계자의 선호도와 에이전트의 목표를 구분하여 두 개의 보상함수를 상정하는 것이 바람직하다.
  • 두 개의 보상함수 상정
    • 외적 보상 함수 (Extrinsic Reward)
      • 설계자의 선호도를 반영한 외부 환경과의 상호작용을 통해 얻는 보상
      • 예 : 방에 얼마나 깨끗한지, 방의 청결도를 최대화하고자 하는 것
    • 내적 보상 함수 (Intrinsic Reward)
      • 에이전트 내부에 설정된 보상
      • 에이전트의 목표나 학습 과정을 효율적으로 유도하는 것
      • 예 : 에이전트가 청소 작업을 효율적으로 하기 위해 새로운 장소를 탐색하거나 장애물을 피하고자 하는 것
    • 위 두가지의 보상 함수를 조합하여 사용한다.
  • 보상 함수 기술
    • 역강화 학습 (Inverse Reinforcement Learning, IRL)
      • 목적: 전문가의 행동 데이터를 통해 외부 보상 함수를 추정하는 방법.
      • 과정: 전문가의 행동을 관찰하여 그들이 어떤 보상 함수를 최대화하려고 하는지를 역으로 추정함.
      • 상관관계: IRL은 주로 외부 보상 함수를 추정하는 데 사용될 수 있음. 전문가의 행동을 통해 설계자의 선호도를 반영한 보상 함수를 도출한다.
    • 보상 셰이핑 (Reward Shaping)
      • 목적: 에이전트의 학습을 가속화하고 효율적으로 만들기 위해 내부 보상 함수를 조정하는 방법.
      • 과정: 기존의 보상 함수에 추가적인 보상이나 페널티를 부여하여 학습을 용이하게 한다.
      • 상관관계: 내부 보상 함수를 설계할 때 유용. 에이전트의 행동을 보다 효율적으로 유도하기 위해 보상 함수를 조정한다.
    • 선호 추출 (Preference Elicitation)
      • 목적: 설계자의 선호도를 직접적으로 추출하여 보상 함수에 반영하는 방법.
      • 과정: 설계자가 특정 행동이나 결과에 대해 선호도를 명시하면, 이를 기반으로 보상 함수를 설정한다.
      • 상관관계: 선호 추출은 외부 보상 함수를 설정하는 데 직접적으로 사용될 수 있으며, 설계자의 명시적인 선호도를 보상 함수에 반영한다.
  • 보상 함수 설계 방법
    • 외부 보상 함수 (Extrinsic Reward Function) : 역강화 학습과 선호 추출을 통해 주로 설정됨.
    • 내부 보상 함수 (Intrinsic Reward Function) : 보상 셰이핑을 통해 주로 설정됨
  • 최적 보상 프레임워크 (optimal reward framework)
    • 개요
      • 주어진 보상 함수 공간에서 에이전트의 행동을 최적화하는 보상 함수를 찾는 접근법
      • 설계자의 목정을 달성하기 위해 에이전트가 학습하는 과정에서 최적의 보상 함수를 발견하는 것을 목표로 함
    • 설명
      • 보상 함수 공간 탐색 : 주어진 보상 함수 공간 (설계자가 정의한 여러 후보 보상 함수로 구성) 에서 다양한 보상 함수를 탐색함
      • 다양한 알고리즘을 사용하여 보상 함수 공간을 탐색하고 최적의 보상 함수를 찾는 것
    • 목표
      • 에이전트가 특정 보상 함수를 학습하여 행동을 최적화할 때, 설계자의 목적(외적 보상 함수)을 최적으로 달성할 수 있는 보상함수를 찾는 것
      • 즉, 외적 보상 함수를 최적화하는 내적 보상 함수를 찾는 것
    • 메타 학습 접근법
      • 학습을 학습하는 기법. 모델이 새로운 작업을 빠르게 배우고 적응할 수 있도록 하는 방법을 개발하는 것
      • 내부 학습 (Inner-loop learning)
        • 특정 작업에 대해 에이전트가 학습하는 단계로, 모델은 주어진 작업에 대해 최적의 성능을 내기 위해 학습한다.
      • 외부 학습 (Outer-loop learning)
        • 여러 작업에서의 학습 경험을 통해 모델의 학습 능력을 향상시키는 단계로, 메타 학습모델이 새로운 작업을 더 잘배우도록 하는 과정이다.
      • 초매개변수 (Hyperparameters)
        • 모델의 학습과정을 조정하는 매개변수로, 메타학습에서는 이 매개변수를 학습한다.
        • 이는 모델이 새로운 작업에 빠르게 적응할 수 있도록 도와준다.
      • 최적 보상 프레임워크는 메타 학습 접근법으로, 외부 루프에서는 보상 함수를 최적화하고, 내부 루프에서는 주어진 보상 함수에 따라 에이전트의 행동을 최적화한다.
  • 정책 경사도 보상 설계(PGRD)
    • 개요
      • 정책 경사도 방법을 사용하여 내적 보상 함수를 최적화하는 접근법
    • 설명
      • 정책 경사도 방법: 정책의 매개변수를 조정하여 기대 보상을 최대화하는 방법
      • 내적 보상 함수 최적화: 내적 보상 함수의 매개변수를 조정하여 에이전트의 행동을 개선
    • PGRD 알고리즘 (절차):
      • 초기 정책 및 보상 함수 설정
      • 정책 경사도를 계산하여 정책을 업데이트
      • 내적 보상 함수의 매개변수를 업데이트
      • 반복
  • 결론
    • 강화 학습에서 보상 함수는 단순히 주어지는 것이 아니라, 효과적으로 설계되어야 하는 요소임
    • 상 함수는 설계자의 선호도와 에이전트의 목표를 구분하여 설정해야 하며, 이를 통해 에이전트가 더 나은 성능을 발휘할 수 있도록 해야함.
    • 두 접근법 모두 에이전트의 행동을 개선하기 위해 보상 함수를 학습하고 최적화하는 데 중점을 두며, 최적 보상 프레임워크는 더 넓은 범위의 메타 학습 문제로, PGRD는 구체적인 알고리즘으로 작동함.

댓글남기기

참고