Fundamentals of Reinforcement Learning - 02. Week 2. Markov Decision Processes

Course Introduction

• 문제를 접하게 되었을 때, 가장 중요한 단계가 문제를 Markov Decision Process(MDP) 로 전환하는 것이다.
• 솔루션의 질은 이 전환과 밀접한 관계가 있다.

관련 자료 (RLbook2018 Pages 47-56)

• Finite Markov Decision Processes (유한한 마르코프 결정 프로세스)

  • bandits 문제와 같이 피드백에 대한 평가를 포함
  • 또한 연관성 측면 (다른 상황에서 다른 액션을 선택하는 것) 의 성격도 가지고 있음
    • bandits 문제는 동일 상황에서 다른 액션을 선택하는 것
  • MDP 는 고전적인 정형화된 sequential decision making (순차 결정) 이다.
    • 액션이 즉각적인 보상에만 영향을 주는 것이 아닌,
    • 후속 상황(situations), 에이전트의 상태(states), 미래의 보상 (future rewards) 에 영향을 줌.
    • 그러므로 MDP 는 지연된 보상, 그리고 지연된 보상과 즉각적인 보상 간의 tradeoff (거래합의) 가 필요하다.
  • MDP 수식 관련
    • bandit problems
      • estimate the value $q_*(a)$
    • MDP
      • estimate the value $q_*(s,a)$ : a : action, s : state
      • or estimate the value $\upsilon_*(s)$ : 상태 기반 추정값
  • MDP 는 강화학습 문제에 있어 수학적으로 이상적인 형태
    • 수학적 구조 상 핵심 요소들 : 보상, 가치함수, 벨먼 방정식 등
  • 강화학습은 적용 가능성의 폭과 수학적 취급 용이성 사이에 있어 tradeoff (거래합의) 가 필요하다.

• The Agent-Environment Interface

  

  • MDP 는 목표 달성을 위해 상호작용을 통한 학습 문제에 있어 직접적인 틀이다.
  • 학습자 (learner) 와 결정자 (decision maker) 는 에이전트 (agent) 라 한다.
  • 에이전트 (agent) 밖의 모든 구성으로 상호작용을 하는 것을 환경 (environment) 이라 한다.
  • 상호작용은 연속적으로 발생한다.
    • 에이전트는 액션을 선택하고 환경은 액션에 반응한다.
      • 환경은 새로운 상황을 에이전트에 제공한다.
      • 환경은 에이전트에 보상을 제공한다.
      • 보상은 특정한 수치값으로 에이전트가 액션을 선택하는 것을 통해 최대화하길 원하는 값이다.
    • 특별히, 에이전트는 환경과 이산적 타임스텝 (0, 1, 2, 3) 의 순서로 상호작용한다고 가정한다.
      • 많은 아이디어들이 시간 연속적인 것이 될 수 있어도, 단순성을 유지하기 위해 케이스를 제한한다.
    • 각 타임스텝 t 에 따라…
      • agent 는 환경의 상태 (environment’s state) 값을 받음 : $S_t \in$ S
      • 이에 따라 agent 는 액션을 선택함 : $A_t \in$ A$(s)$
      • 액션에 따른 결과로 에이전트는 수치적 보상을 얻음 : $R_{t+1} \in R \subset$ R
      • 이후 다른 환경의 상태 값을 제공받음 : $S_{t+1}$
    • 위에 따라 MDP 와 에이전트는 아래와 같은 시퀀스, 혹은 궤적 (trajectory) 를 남기게 됨
      • $ S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, R_3, …$

  

  • 유한 MDP (finite MDP) 에서 모든 상태, 액션, 보상의 집합은 유한한 수의 요소 (element) 이다.
  • $R_t$ 와 $S_t$ 는 이전 상태와 액션값에만 영향을 받는 이산확률분포 (discrete probability distributions) 로 정의됨
    • 이산확률분포 : 확률변수가 가질 수 있는 값이 명확하고 셀 수 있는 경우의 분포 (주사위의 눈 $1, …, 6$)
    • 연속확률분포 : 확률변수가 가질 수 있는 값이 연속적인 실수여서 셀 수 없는 경우의 분포 ($y = f(x)$)
  • 우선 제공된 state 와 action 에 따른 time t 시점의 확률 값이 존재 (상단 수식)
  • 모든 $s’, s \in S, r \in R, a \in A(s)$ 에 대해 function $p$ 는 dynamics of the MDP 로 정의된다.
  • 일반적인 함수 표현, The dynamics function $p : S \times R \times S \times A \to [0,1]$
  • | : 조건부 확률에 대한 표기법이지만, 여기서는 $p$ 가 $s, a$ 의 각 선택에 대한 확률분포를 지정한다는 것을 뜻함.

  

  • MDP (Markov decision process) 에서 $p$ 로 주어진 확률은 환경의 역학을 완벽히 특성화함.
    • 즉, 가능한 $S_t$, $R_t$ 값에 대한 가능성은 이전에 즉시 제공된 $S_{t-1}$, $A_{t-1}$ 값에만 의존한다.
    • 그 이전의 상태값과 액션은 영향을 주지 않는다.
    • 이것은 결정 과정에 대한 제한이 아닌 상태에 대한 제한을 의미한다.
    • 상태에 미래의 차이를 발생 시킬 수 있는 이전 에이전트-환경 간 상호작용에 대한 측면이 모두 정보로 포함되어 있어야 한다.
    • 만약 그렇다면, 이 상태를 마르코프 속성 (Markov property) 이라 한다.
      • 이후 과정에서 Markov 속성에 의존하지 않는 근사 방법 (approximation methods) 을 고려할 것
      • 17장에서는 Markov 가 아닌 관찰값으로부터 어떻게 Markov 상태를 구성하고 학습할지를 고려할 것
    • 4개의 인수를 가진 dynamic function $p$ 에서 state-transition probabilities (상태 전이 확률) 와 같은 알고싶은 모든 것을 계산할 수 있음.

    

    $p : S \times S \times A \to [0,1]$

    • 또한 예상되는 보상값을 2개 인자 (state,action) 의 r 함수로 계산할 수 있음.

    

    $r : S \times \ A \to R$

    • 예상되는 보상값을 3개 인자 (state, action, next state) 의 r 함수로 계산할 수 있음.

    

    $r : S \times \ A \times S \to R$

    • 이 책에서 우리는 주로 4개 인자의 $p$ 함수 (3.2) 를 사용하지만 때때로 다른 함수가 편리할 경우도 있음.

    • MDP 프레임워크는 추상적이고 유연하여 다양한 문제에 적용할 수 있음
      • 스텝 (Step) 은 고정된 시간 간격일 필요가 없음. 의사 결정과 행동의 임의적 연속 단계일 수 있음
      • 동작 (Action) 은 로봇 팔의 모터 전압과 같이 낮은 수준의 제어부터 대학원에 갈 것인지 여부를 정하는 높은 수준의 결정일 수 있음.
      • 상태 (State) 는 직접적인 센서의 데이터처럼 낮은 수준의 감각일 수 있고, 방에 있는 물체에 대한 상직적 설명과 같이 높은 수준의 추상일 수 있음.
      • 또한 상태 (State) 는 과거 감각의 기억이거나 정신적, 주관적인 것일 수 있음.
        • 예를 들어 에이전트는 물체가 어디있는지 확신하지 못할 수 있음
      • 액션 (Action) 은 정신적일수도, 계산적일 수도 있음
        • 일부 동작은 에이전트가 어디에 집중할지 를 변경하는 것일 수 있음
      • 즉 액션은 우리가 결정을 내리는 방법을 배우고자 하는 모든 결정, 상태는 결정을 내리는 데 유용한 모든 것이 될 수 있음.
    • MDP 에서 에이전트와 환경의 경계는 일반적인 물리적 경계와 동일하지 않음.
      • 대게 경계는 중간지점보다 에이전트에 더 가깝게 그려짐
        • 예를 들어 로봇의 기계적 감지 하드웨어는 에이전트의 일부가 아닌 환경의 일부로 간주되어야 함.
        • 생물체일 경우 근육, 골격 및 감각 기관은 환경의 일부로 간주되어야 함.
      • 보상 또한 인공 학습 시스템 본체 내부에서 계산되지만, 에이전트 외부에 있는 것으로 간주됨.
    • 즉, 에이전트가 임의로 변경할 수 없는 모든 것은 환경의 일부로 간주한다는 것임.
      • 에이전트는 환경의 일부를 알고 있음
        • 에이전트는 자신의 행동과 상태에 대해 보상이 어떻게 함수로 계산되는지에 대해 알고 있음.
        • 그러나 보상 계산은 에이전트 밖의 영역임.
        • 우리가 루빅큐브가 어떻게 작동하는지 알지만, 여전히 해결할 수 없는 문제가 될 수 있는 것처럼
        • 환경이 어떻게 작동하는 지에 모든 것을 알고있으면서도 여전히 어려운 강화 학습 작업에 직면할 수 있음.
      • 즉, 에이전트와 환경의 경계는 에이전트의 지식이 아닌 제어의 한계를 나타냄.
    • 에이전트와 환경의 경계는 서로 다른 목적을 위해 다르게 위치할 수 있음
      • 복잡한 로봇을 예로 들면 각각 고유한 경계를 가진 여러 에이전트가 한번에 작동할 수 있음
        • 높은 수준의 결정을 구현하는 에이전트가 낮은 수준의 에이전트가 직면한 상태의 일부를 형성하는 높은 수준의 결정을 내릴 수 있음
      • 에이전트와 환경 간의 경계는 상태, 액션, 보상을 결정한 뒤 결정을 위한 관심사를 식별한 뒤에 정해짐.
    • 즉, MDP 프레임워크는 상호작용으로부터 목표 지향적 학습을 하는 문제를 추상화한 것이다.
      • 감각, 기억, 제어 장치의 세부사항이 무엇이든
      • 달성하려는 목표가 무엇이든
      • 목표 지향적 행동을 학습하는 문제는 에이전트와 그 환경 사이를 오가는 3가지 신호로 축소될 수 있다고 제안하는 것.
        • Actions : 에이전트의 선택을 나타내는 신호
        • States : 선택이 이루어지는 기준(상태) 를 나타내는 신호
        • Rewards : 에이전트의 목표를 정의하는 신호
    • 이 프레임워크는 모든 의사결정 학습문제를 유용하게 나타내기에 충분하지 않을 수 있지만, 널리 이용 가능하고 적용 가능한 것으로 입증됨.
      • 물론 states 와 actions 는 작업마다 크게 다르며, 이것을 표현하는 방식이 성능에 큰 영향을 줌
      • 다른 종류의 학습과 마찬가지로 강화학습에서 이러한 표현 선택은 과학보다 예술에 가까움.
      • 이 책에서 우리는 상태와 행동을 나타내는 좋은 방법에 관한 몇 가지 조언과 예를 제공하지만,
      • 우리의 주요 초점은 일반적인 원칙 (표현법이 선택되면 그것이 어떻게 동작하는지) 을 배우는 것에 있음.
    • 예제 3.1 : Bioreactor (바이오 리액터 - 세포배양기)
      • 강화 학습이 세포배양기의 순간 온도와 교반 속도 (뒤섞는 교반기의 회전 속도) 를 결정하기 위해 적용되어 있다고 가정
      • Actions : 목표 온도와 목표 교반속도를 달성하기 위해 발열체와 모터를 직접 조종하는 하위 제어시스템에 전달되는 값
      • States : 여과되고 지연된 열전대, 기타 센서 값과 대상 화학물질을 나타내는 상징적 입력값 등
      • Rewards : 유용한 화합물이 생성되었는지에 대한 순간적인 측정값
      • 여기서 상태 값은 list 혹은 vector 값 (센서 측정값, 상징적 입력값)
      • 액션 값은 vector 값 (목표 온도와 교반속도로 이루어진)
      • 보상 값은 항상 단일 숫자값
    • 예제 3.2 : Pick-and-Place Robot
      • 반복적인 물체 이동 작업에서 로봇 팔의 동작을 제어하기 위해 강화학습을 사용한다고 가정
      • 빠르고 부드러운 동작을 학습하려면 학습 에이전트가 모터를 직접 제어하고, 기계 연결장치의 현재 위치와 속도에 대한 짧은 지연시간의 정보를 가져와야 함
      • Actions : 각 관절의 모터에 적용되는 전압
      • States : 관절의 각도와 속도의 최신 값
      • Rewards : 잘 운반된 개체에 대해 + 1 값
      • 부드러운 움직임을 장려하기 위해 각 단계의 순간순간의 갑작스러운 움직임에 작은 처벌 (보상의 음수값) 을 부여
    • 예제 3.3 : Recycling Robot (재활용 로봇)
      • 모바일 로봇은 사무실 환경에서 빈 음료수 캔을 모으는 일을 함
      • 로봇은 캔을 감지하는 센서, 캔을 집어 일체형 통에 넣을 수 있는 팔과 그리퍼를 가지고 있음
      • 로봇은 충전식 배터리로 작동
      • 로봇의 제어 시스템에는 센서 정보를 해석하는 파츠, 탐색기능 파츠, 팔과 그리퍼를 컨트롤 하는 파츠 가 있음.
      • 높은 수준의 의사결정 (빈 캔을 어떻게 찾을지) 은 현재 배터리 충전 레벨에 따라 강화학습 에이전트가 내림.
      • 간단한 예제를 만들기 위해 충전정도는 2가지 레벨만 구분한다고 가정, 작은 상태 집합 $S = \lbrace high,low \rbrace$ 으로 구성
      • 각 상태에서 에이전트는 다음 중 하나의 결정을 할 수 있음.
        • (1) 일정 시간 동안 적극적으로 캔을 찾음
        • (2) 움직이지 않고 누군가가 캔을 가져올 때까지 기다림
        • (3) 배터리 충전을 위해 충전 장소로 돌아감
      • 배터리가 많이 남았을 때 (high), 충전은 언제나 멍청한 선택이므로 해당 상태의 action set 으로 포함시키지 않는다.
        • action set 은 $A(high) = \lbrace search,wait \rbrace$ 와 $A(low) = \lbrace search, wait, recharge \rbrace$ 이다.
      • 대부분의 경우 보상은 0 이지만, 로봇이 빈 캔을 확보하면 (+), 배터리가 완전히 방전되면 큰 수치의 (-) 가 됨.
      • 캔을 찾는 가장 좋은 방법은 능동적 탐색이지만 배터리가 소모됨 (배터리가 고갈될 가능성이 있음)
      • 기다리는 것은 배터리가 소모되지 않음
      • 배터리가 고갈되면 로봇은 종료되고 구조될 때까지 기다려야 함 (낮은 보상 생성)
      • 배터리가 많으면 배터리 고갈 위험 없이 빈 캔 탐색을 완료할 수 있음
        • 배터리가 많을 때의 탐색 기간에서 배터리가 많이 남아 있을 확률 $\alpha$
        • 배터리가 많을 때의 탐색 기간에서 배터리가 적어질 확률 $1 - \alpha$
      • 반대로 배터리가 적으면
        • 배터리가 적을 때의 탐색 기간에서 배터리가 적어질 확률 $\beta$
        • 배터리가 적을 때의 탐색 기간에서 배터리가 고갈될 확률 $1 - \beta$
      • 후자의 경우 로봇은 구조되어야만 하며, 이 경우 배터리는 다시 완충된다.
      • 로봇에 의해 수집된 캔의 수량 만큼 보상이 주어지며, 로봇이 구출되었을 때 보상값 -3 이 주어진다.
      • $r_{search}, r_{wait}$ with $r_{search} > r_{wait}$ : 로봇이 검색 혹은 대기 중에 수집할 것으로 추정되는 캔 수 (즉, 예상되는 보상)
      • 충전을 위해 충전 장소로 돌아갈 때나, 배터리가 고갈되었을 때에는 캔을 회수할 수 없음
      • 이 시스템은 유한한 MDP 이며 전확 확률과 예상 보상을 아래와 같이 표기할 수 있다.

      

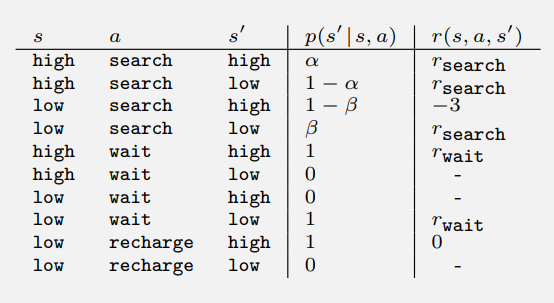
      • 위 표는 현 상태 $s$, 액션 $a \in A(s)$, 다음 상태 $s’$ 의 각각의 가능한 조합으로 구성된 표이다.
      • 몇몇 전환은 일어날 가능성이 0 이므로, 기대되는 보상 또한 없다.

      

      • 위 그래프는 transition graph 로, 유한 MDP 의 역학을 요약하는 또다른 방법이다.
      • state nodes 와 action nodes 가 있음.
      • state nodes : 큰 빈 원, 원 안에 라벨링 된 이름
      • action nodes : 작은 검은색 원과 state nodes 를 연결 시키는 화살표
      • 상태 $s$ 에서 작업 $a$ 를 수행하면 상태노드 $s$ 에서 작업노드 $(s,a)$ 로 이동함.
      • 그 다음 환경은 $(s,a)$ 를 떠나는 화살표 중 하나를 통해 다음 상태의 노드 $s’$ 로 전환시킴
      • 각 화살표는 $(s, s’, a)$ 에 해당함.
      • 여기서 $s’$ 는 다음 상태이고, 전환확률 $p(s’|s,a)$ 와 해당 전환에 대한 예상보상은 $r(s,a,s’)$ 임.
      • 작업 노드를 떠나는 화살표의 전환 확률의 합계는 항상 1임.

• Goals and Rewards

  • 강화학습의 목적, 목표는 특별한 신호로 정형화 되는데 이를 보상 (Reward) 이라 하고 환경이 에이전트에 전달하는 값이다.
  • 각 스텝마다 보상은 단순한 숫자 값이다. $R_t \in R$
  • 비공식적으로, 에이전트의 목표는 총 보상의 양을 최대화 하는 것이다.
    • 이 최대화의 의미는 당장의 보상을 최대화 하는 것이 아닌 장기적 누적 보상을 최대화 하는 것이다.
  • 보상 측면에서 위 목표를 공식화하는 것이 처음에는 제한적으로 보일 수 있지만, 실은 유연하고 광범위하게 적용될 수 있다.
    • 예 1. 로봇이 걷는 법을 배움 : 보상은 로봇이 전진할 때마다 주어짐
    • 예 2. 로봇이 미로를 통과하는 법을 배움 : 매 스텝마다 -1 의 보상을 주어 에이전트가 최대한 빨리 미로를 탈출하는 것을 장려한다.
    • 예 3. 재활용 캔 수집을 하는 법을 배움 : 캔을 모을 때마다 +1 의 보상을 주며, 뭔가에 부딪히거나 누군가 소리를 지를 경우 - 보상을 준다.
    • 예 4. 체스 두는 법을 배움 : 이길 때 +1점, 질 때 -1점, 비길 때 0점의 보상을 부여
  • 즉, 에이전트가 우리의 목표를 달성하게 하기 위해 최대화 할 수 있는 보상을 제공해줘야 한다.
    • 따라서 보상이 정말 우리가 원하는 결과를 나타내는 것인지가 매우 중요하다.
  • 보상은 우리가 원하는 것을 달성하기 위한 사전지식을 전달하는 곳이 아니다.
    • 이것에 적합한 위치는 초기 정책 또는 초기 가치 함수, 혹은 이들에 영향을 줄 수 있는 값이다.
    • 예를 들어 체스 게임일 경우 상대의 말을 잡거나 센터를 장악하는 것에 보상이 주어저서는 안 된다.
      • 에이전트는 승패의 여부와 관계없이 이 서브 목표를 달성하는 것을 학습할 것이다.
    • 즉, 보상은 에이전트에게 달성해야 하는 것에 대한 소통을 하는 방법이고, 어떻게 달성할지에 대한 것을 이야기 하는 것이 아니다.

• Returns and Episodes

  

  • 정확히 시퀀스의 어떤 면을 최대화 하길 원하는지에 대하여, 가장 단순히 보상의 합계를 표현한 형태
  • final time step $T$ 라는 개념이 있을 경우
    • 환경과 에이전트 간 상호작용이 자연스럽게 끊길 때, 우리는 이것을 에피소드 (episode) 라 표현
    • 예를 들어 게임 한 판, 하나의 미로를 통과하는 것 혹은 어떠한 종류의 반복적인 상호작용 등
  • 에피소드가 끝난 상태를 terminal state 라 한다.
    • 이후 표준 시작 상태로 재설정하거나, 시작 상태의 표준 분포에서 샘플을 재설정한다.
    • 에피소드가 다른 방식으로 끝나더라도 (예를들어 게임에서의 승리,패배) 다음 에피소드는 이전 에피소드와 독립적으로 시행된다.
    • 즉 에피소드는 모두 terminal state 로 끝나나, 보상과 결과는 다를 수 있다.
  • 위와 같은 에피소드 형태의 일을 episodic tasks 라 한다.
    • $S$ : 모든 non-terminal state
    • $S^+$ : 모든 non-terminal state + terminal state
    • $T$ : The time of termination
  • 반면 많은 경우 환경과 에이전트의 상호작용은 자연스럽게 별개의 에피소드로 끊기지 않는다.
    • 이를 continuing tasks 라 한다.
    • final time step $T=\infty$ 이기 때문에 위 3.7의 수식으로 표현할 수 없다.
    • (우리가 최대화를 원하는 리턴 값이 쉽게 무한대의 값이 될 수 있다.)
    • 즉, discounting 이라는 추가적 개념이 필요하다.

  

  • 에이전트는 미래의 할인된 보상값의 합 (sum of the discounted rewards) 이 최대값이 되도록 액션 ($A_t$)을 선택한다.
  • $0 \le \gamma \le 1$ 인 $\gamma$ 파라미터를 discount rate 라 한다.
  • discount rate 는 미래 보상의 현재 가치를 결정한다.
    • 미래 $k$ time steps 에서 받을 보상은 현재의 가치로 따졌을 때 $\gamma^{k-1}$ 배의 가치만 있다.
    • $\gamma < 1$ : 극한 합 (3.8) 의 값이 유한한 값으로 수렴한다. ($R_k$ 가 제한된 값일 경우)
    • $\gamma = 0$ : 에이전트는 오직 $A_t$ 를 선택해 $R_{t+1}$ 값을 최대화하는 방법만을 학습한다. (근시안적)
    • $\gamma \to 1$ : 1에 가까워질 수록 미래의 보상값을 더 강하게 계산. (원시안적)

  

  • 연속적인 time step (successive time step) 에서의 보상은 상호간 연관관계에 있고, 이는 강화학습에서 중요한 개념이다.
  • 위 공식은 모든 time steps $t < T$ 에서 적용되며, 심지어 $t + 1$ 에서 termination 이 일어나는 경우에도 $G_T = 0$ 으로 정의함으로써 적용가능하다.
  • 3.8 의 인자 수가 무한대이지만, 보상이 0 이 아니고 상수 일 경우 여전히 유한한 숫자가 된다.
    • 예를 들어 보상이 상수 $+1$ 이고 , $\gamma < 1$ 일 경우 보상 값은 아래의 값이 된다.

  • 예제 3.4 : Pole-Balancing

    

    • 목표 : 카트에 힘을 적용하여 트랙 위를 카트가 이동할 수 있되, 폴이 서 있고 넘어지지 않게 유지하는 것
    • 실패 : 폴이 주어진 각도를 넘어서 넘어지는것 혹은 카트가 트랙에서 탈선하는 것
    • 폴은 매 실패 이후 리셋되어 수직으로 서게 된다 > 이 일은 episodic 으로 간주될 수 있음
      • 자연스러운 에피소드가 반복됨
      • 보상은 실패하기 전 모든 타임 스텝에 +1 을 줄 수 있다.
    • 위의 설정은, 폴이 영원히 성공적으로 벨런스를 잡게 되면 보상은 무한수가 된다는 뜻이다.
    • 또는 위 문제를 continuing task 로 간주할 수도 있다. (using discounting)
      • 위의 경우 실패할 경우 보상은 -1 이 되고, 그 외에는 0 이 된다.
      • 즉 보상 값은 $- \gamma^K$ 가 되며, $K$ 는 실패 이전의 타임스텝이 된다.
    • 양쪽의 경우 모두 폴의 균형을 최대한 유지할 수록 보상이 최대화 된다.

Introduction to Markov Decision Processes

• 학습목표
  • Markov Decision Process (MDP) 에 대해 이해하기
  • MDP 프로세스가 정의되는 방법 이해
  • Markov Decision Process 의 그래픽 표현 이해
  • MDP 프레임워크로 다양한 프로세스를 작성하는 방법
• Markov Decision Processes
  • k-Armed Bandit Problem : 같은 상황에서 같은 Action 이 항상 최적화된 선택이 되는 문제유형 (현실과 다름)
    • 예 : 토끼의 왼쪽에 브로콜리 (보상 : +3) 가 있고 오른쪽에 당근 (보상 : +10) 이 있을 경우
    • 토끼는 오른쪽의 당근을 먹는 것을 선택한다.
    • 갑자기 두 음식의 위치가 바뀔경우 k-Armed Bandit Problem 으로 정의할 수 없는 문제가 된다.
  • 현실 : 다른 상황이 다른 반응을 야기하며, 현재 선택한 Action 이 미래의 보상의 양을 결정한다.
    • 예 : 토끼의 왼쪽에 브로콜리 (보상 : +3) 가 있고 오른쪽에 당근 (보상 : +10) 이 있을 경우
    • 단, 오른쪽 방향에 호랑이가 있음
    • 장기적 이익 관점에서 토끼는 브로콜리를 선택해야 한다. (즉각적 보상이 적다 하더라도)

  

  • The dynamics of an MDP
    • 출처 : Coursera / Fundamentals of Reinforcement Learning / W2. Markov Decision Process / 동영상 : Markov Decision Processes
    • The dynamics of an MDP : 확률 분포에 의해 정의됨.
• Examples of MDPs
  • Recycling Robot 에 대한 예시
    • State : 배터리 잔량 High, 배터리 잔량 Low
    • Action :
      • 배터리 잔량 High : Search, Wait, Recharge
      • 배터리 잔량 Low : Search, Wait

  

  • Dynamics_of_the_Recycling_Robot
    • 출처 : Coursera / Fundamentals of Reinforcement Learning / W2. Markov Decision Process / 동영상 : Examples of MDPs
  • MDP 는 다양한 문제에 적용이 가능하다.

Goal of Reinforcement Learning

• 학습목표
  • 에이전트의 목표와 보상이 어떻게 관련되는지 설명
  • 에피소드에 대한 이해 및 에피소드로 표현될 수 있는 작업 식별
• The Goal of Reinforcement Learning
  • Bandits Problems : 즉각적 보상의 최대화
  • MDP : 타임스텝 전체의 보상 합의 최대화
    • 토끼가 오른쪽의 당근을 먹는 것은 즉각적 보상의 최대화를 야기하나 이후 바뀐 상태에 의해 호랑이에 잡아먹힘
    • 로봇에게 걷는 방법을 가르쳐 줄 때, 보상 값이 앞으로 나아간 수치라 하여 이를 즉각적으로 최대화 할 경우 넘어져 걷질 못하게 됨
  • Episodic Tasks : 마지막 스텝을 밟은 뒤 다시 초기상태로 돌아감 (에이전트-환경 간 상호작용의 종료)
    • 체스게임
• Michael Littman: The Reward Hypothesis
  • Reinforcement Learning 에서 보상을 정의하는 것
    • 물고기를 주면 하루를 먹고 : Programming (Good Old-Fashioned AI) > 새로운 환경에서 새 프로그래밍을 해야 함
    • 물고기를 잡는 법을 알려주면 평생을 먹고 : Supervised Learning > 학습 데이터를 제공해야 함
    • 물고기의 맛을 알려주면 어떻게 물고기를 잡을지 알아낸다. : Reinforcement learning > 최적화문제
    • Ashraf : All goals can be described by the maximization of expected cumulative rewards
    • Silver : All goasl can be described by the maximization of expected cumulative rewards
    • Sutton : What we mean by goals and purposes can be well thought of as maximization of the expected value of the cumulative sum of a received scalar signal (reward).
  • 강화학습의 정의
    • Intelligent behavior arises from the actions of an individual seeking to maximize its received reward signals in a complex and changing world.
      • identify where reward signals come from,
      • develop algorithms that search the space of behaviors to maximize reward signals.
    • 보상은 복잡한 실 세계 속에서 단순해야 한다.
    • 에이전트가 최적화해야 할 보상이 무엇인지 알아내야 한다.
    • 위 보상을 최대화 할 알고리즘을 디자인해야 한다.
  • 보상 정의의 어려움
    • 공통 통화 정의의 어려움
      • 온도조절장치 제어의 경우 : 난방/에어컨 등의 에너지 비용 vs 거주자의 불편도?
      • 위의 정도를 달러로 표기? (자연스럽지가 않음)
    • 하나의 예는 목적을 달성했을 때 +1, 그렇지 않은 경우 0 (goal reward Representation)
    • 반대로 목적이 달성하지 않았을때 매 스텝마다 -1 (action penalty Representation)
  • 보상의 정의 방식에 따른 차이 발생
    • Goal-reward Representation : 긴급함이 없음
    • Action-Penalty Representation : 진행이 막혀 더이상 목적을 달성할 수 없는 확률이 있을 경우 오작동
    • 두 경우 모두 흐름이 길 경우 큰 문제가 발생함.
    • 어떠한 중간 보상은 에이전트가 올바른 방향으로 학습하는데 큰 도움이 될 수도 있음
    • 보상의 출처가 사람일 경우
      • 사람은 보상 기능과 다르게 에이전트가 학습하는 방식에 따라 보상을 변경하는 경향이 있음 (Non-stationary Rewards)
        • 고전적인 강화학습 알고리즘은 위와 같은 경우 잘 적용되지 않음
  • 보상의 지정
    • 프로그래밍 방식
      • 학습 에이전트에 대한 보상을 정의하는 가장 일반적인 방법
      • 예 : 상태를 가져오고 보상을 출력하는 프로그램을 작성
      • 프로그래밍 언어의 예 - temporal logic : 사람과 기계 언어의 중간 지점
    • 예를 들어 사람이 주는 보상을 복사하는 방법을 배우는 것 : Mimic reward
    • 이 접근 방식의 흥미로운 버전 : 역 강화학습 : Inverse Reinforcement Learning
      • 역 강화학습에서 지도자는 원하는 행동의 예를 보여주고 학습자는 지도자가 이 행동을 최적으로 만들기 위해 최대화한 보상이 무엇인지 파악
      • 강화학습이 보상에서 행동으로 진행되는 반면, 역강화학습은 행동에서 보상으로 진행됨.
      • 일단 보상이 식별되면 이러한 보상은 다른 설정에서 최대화 될 수 있으므로 환경 간에 강력한 일반화가 가능함.
    • 최적화 프로세스를 통해 간접적으로 파생되는 보상
      • 점수를 생성할 수 있는 높은 수준의 행동이 있는 경우
      • 해당 행동을 장려하는 보상을 고려할 수 있음
    • Meta reinforcement learning
      • 동 목표를 수행하는 단일 에이전트가 아닌 다수 에이전트가 있을 경우
      • 행동의 결과로 보상을 받는 것 뿐만 아닌 이 행동에 대한 인센티브로 보상을 사용하여 평가할 수 있게 함
      • 강화학습 에이전트는 더 좋은 보상 기능과 이를 최대화하기 위한 더 좋은 알고리즘이 있는 경우 생존함
      • 개별 수준에서 더 나은 학습 방법을 만드는 진화 수준에서의 학습방법
      • 에이전트가 자손에게 보상 함수를 계승함
  • 보상 이론의 도전과제
    • 보상을 극대화 하는 것 이외에 다른 일을 하는것 처럼 보이는 행동의 예
      • 위험 회피 행동 : 최선이 아닐 수 있지만 최악의 결과가 발생할 가능성을 최소화 하는 행동을 선택
    • 원하는 행동이 항상 최선의 것이 아니라 여러 가지를 균형있게 수행하는 것이라면?
      • 예 : 음악 추천 시스템 (최근 재생된 곡의 경우 그 곡에 대한 보상이 줄어야 함)
    • 올바른 결정이 단순히 하나의 목표를 추구하는 것이 아니라면?
      • 더 나은 목표를 만드는 것
    • 그럼에도 보상을 극대화 하는 것이 지능형 에이전트에게 동기를 부여하는 훌륭한 근사치일 수 있다는 가능성을 염두

Continuing Tasks

• 학습목표
  • 연속적인 작업에 대해 할인을 이용한 보상의 수식화
  • 연속적인 time step 에서 보상이 상호간 어떻게 관련되어 있는지 확인
• Continuing Tasks

  • Episodic tasks 와 달리 현실에서는 에이전트와 환경이 계속 상호작용 하는 경우 (Continuing) 가 많다.

    Episodic Tasks	Continuing Tasks
    상호작용이 자연스럽게 끝남	상호작용이 계속 유지됨
    각각의 에피소드는 Terminal State 로 끝남	Terminal state 가 없음
    에피소드는 상호독립적임
    $G_t \doteq R_{t+1} + R_{t+2} + R_{t+3} + … + R_T$	$G_t \doteq R_{t+1} + R_{t+2} + R_{t+3} + …$ (무한)

  • 예 ) 건물 안 온도조절기 : 환경과의 상호작용에 끝이 없음.
    • 상태 : 시간, 건물 내 사람 수
    • 액션 : 켜기, 끄기
    • 보상 : 누군가가 온도를 수동조절 할 경우 -1, 그렇지 않은 경우 0
  • State 가 무한함에 따라 보상의 합이 무한으로 발산하는 것을 방지하기 위해 Discounting 을 한다.
    • Discounting 계수 $\gamma$ , $0 \leq \gamma < 1$
    • $G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + … + \gamma^{k-1} R_{t+k} + … = \sum_{k=0}^\infty\gamma^k R_{t+k+1}$
    • 이것은 현재의 1 달러가 1년 뒤에 받을 1달러 보다 가치가 있다고 생각하면 이치에 맞는다.
    • $G_t$ 가 무한하지 않음 (Finite) 을 증명하는 수식
      • $G_t = \sum_{k=0}^\infty\gamma^k R_{t+k+1} \leq \sum_{k=0}^\infty\gamma^k R_{max} = R_{max} \sum_{k=0}^\infty\gamma^k = R_{max} \times {1 \over 1-\gamma}$
    • $\gamma$ 값에 따른 에이전트의 성향
      • $\gamma = 0$ : 즉각적인 보상만을 추구하는 에이전트 (Short-sighted)
      • $\gamma \to 1$ : 미래의 보상을 중시함 (Far-sighted)
  • Return 값의 재귀적 표현법
    • $G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + … = R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + \gamma^2 R_{t+4} + … )$
    • $G_t = R_{t+1} + \gamma G_{t+1}$