Fundamentals of Reinforcement Learning - 04. Week 4. Dynamic Programming

관련 자료 (RLbook2018 Pages 73-88)

• Dynamic Programming
  • 동적 프로그래밍이란?
    • Markov decision process (MDP) 형태의 완벽한 환경 모델이 제공될 때 최적 정책을 계산하기 위한 알고리즘의 집합
    • 완벽한 모델이라는 가정과 비싼 컴퓨팅 비용 때문에 전통적 동적 프로그램 (DP) 은 강화학습에서 활용성이 떨어짐
    • 하지만 이론적으로 여전히 중요함 (필수적인 기초 지식)
      • 모든 방식들이 위의 2가지 제약을 벗어나 DP (Dynamic Programming) 와 동일한 효과를 내는 것을 시도하는 것이라 볼 수 있다.
  • 주로 사용하는 동적 프로그래밍의 환경 조건
    • a finite MDP (유한 MDP)
      • state sets $S$, action sets $A$, reward sets $R$ 은 유한함
      • 환경의 역학 (dynamics) 은 확률의 집합 $p(s’,r|s,a)$ 로 제공됨 ($s \in S, a \in A(s), r \in R, s’ \in S^+$)
        • $S^+$ 는 $S$ 에 terminal state 를 포함한 것 (episodic task 일 경우)
    • 비록 DP 가 continuous state, action spaces 에서도 적용할 수 있다 해도 그것은 특이 케이스인 경우 뿐임.
      • continuous state 에서 DP를 적용하는 통상의 방법은 state 와 action을 quantize (근사) 하여 유한 상태의 DP 방식을 적용하는 것이다.
  • DP, 그리고 일반적인 강화학습의 핵심 아이디어는 가치 함수를 사용하여 좋은 정책을 찾기 위한 구조화를 하는 것이다.
    • 우리는 최적 정책을 벨만 최적 방정식을 만족하는 최적 가치함수를 구함으로서 쉽게 찾을 수 있다.

    

    • for all $s \in S$, $a \in A(s)$, $s’ \in S^+$
    • DP 알고리즘은 벨만 방정식을 원하는 가치함수 (최적가치함수) 의 근사값을 개선하는 업데이트 규칙으로 전환한다.
• Policy Evaluation (Prediction)
  • 첫번째로 임의의 정책 $\pi$ 의 상태 가치 함수 $v_{\pi}$ 를 계산하는 방법을 고려한다.
    • 이것을 DP (Dynamic Programming) 용어로 정책 평가 (Policy evaluation) 이라 한다.
    • $v_\pi$ 의 고유성은 $\gamma < 1$ 혹은 정착 $\pi$ 아래 모든 상태에서 필연적인 종료 (termination) 가 보장될 경우 보장된다.
    • 만일 환경의 역학을 완전히 알 경우 (4.4) 는 $|S|$ 개의 미지수를 가진 선형 방정식으로 풀릴 수 있다.
      • 이는 직관적이지만 지루한 연산 과정이다.
  • 우리의 목적을 달성하기 위해 반복 솔루션 방법이 가장 적합하다.
    • $S^+$ 와 $R$ (실제 숫자 값) 을 매핑하는 근사 가치함수 $v_0, v_1, v_2, …$ 를 가정한다.
    • 최초의 근사, $v_0$ 는 임의로 선택 (단, 최종 상태가 있는 경우 0을 지정)
    • 각 연속적인 근사치는 벨만 방정식의 업데이트 규칙을 사용하여 얻음.
    • $v_\pi$ 에 대한 벨만 방정식이 등치를 보장하기 때문에, 모든 $s \in S$ 에 대해 $v_k = v_\pi$ 는 위 업데이트 규칙의 고정점이다.
    • 사실 시퀀스 $\lbrace v_k \rbrace$ 는 일반적으로 $k \to \infty$ 에 따라 $v_\pi$ 로 수렴한다.
    • 위 알고리즘을 반복 정책 평가 (iterative policy evaluation) 라 한다.
  • iterative policy evaluation
    • expected update
      • $v_k$ 로부터 $v_{k+1}$ 연속 근사를 생성하기 위해, iterative policy evaluation 은 각 $s$ 상태에 같은 연산을 적용한다.
      • 평가 중인 정책의 가능한 모든 한 단계의 전환에 대하여…
      • 이전 값 $s$ 를 새로운 값으로 교체하기 위해 $s$ 의 후속상태의 이전 값과 즉각적인 보상을 이용
      • 우리는 이러한 연산을 expected update 라 한다.
      • 위의 각 반복은 모든 상태의 값을 한번 업데이트 하여 $v_k$ 에서 $v_{k+1}$ 을 생성한다.
    • several different kinds of expected updates
      • state 를 업데이트 하거나, state-action pair 를 업데이트 할 수 있음
      • 후속 상태의 추정 값이 결합되는 방법에 따라 달라짐
      • DP 에서 사용하는 모든 업데이트 방식을 expected update 라 한다.
        • 모든 가능한 다음 상태의 추정값에 기반하기 때문 (다음 상태를 샘플링 하는 것이 아닌)
        • 방정식이나 백업 다이어그램 등으로 표현이 가능함.
    • 순차 컴퓨터 프로그램으로 iterative policy evaluation 을 구현하는 방법
      • two-array version
        • 두 개의 array 를 사용 (old values $v_k (s)$, new values $v_{k+1} (s)$)
        • 두 개의 array 를 사용함으로써, 이전 값의 변경 없이 새로운 값을 계산할 수 있음.
      • in-place algorithm
        • 하나의 array 를 사용하여 제자리에서 값을 업데이트 한다.
        • 새로운 값이 즉각적으로 이전 값을 덮어 쓴다.
        • 각 상태의 업데이트 순서에 따라, 이전 값이 아닌 새로운 값을 업데이트에 쓰기도 한다.
        • 이 알고리즘 또한 $v_\pi$ 로 수렴한다.
          • two-array version 보다 더 빠르게 수렴한다.
          • 사용 가능한 새로운 데이터를 즉각 사용하기 때문
          • 업데이트 되는 상태의 순서가 수렴율에 큰 영향을 끼친다.
        • DP 알고리즘에서의 알고리즘은 주로 in-place version 이라 생각하면 된다.
    • in-place version of iterative policy evaluation (pseudocode)
      • 종료 상태를 관리함 (수렴은 극한 값에서 이루어지지만, 이보다 짧아야 함.)
      • 의사코드는 $\max_{s \in S} | v_{k+1} (s) - v_k (s) |$ 의 값을 매 sweep 마다 체크하고, 값이 충분히 작아지면 중지한다.
  • 예제 4.1 : 4 x 4 gridworld
    • 종료상태 미포함 상태 $S= { 1,2,…,14 }$
    • 각 상태에서 가능한 행동 $A = { up, down, right, left }$
    • 행동에 따라 결정론적으로 상태의 전이가 일어남 (그리드를 벗어나는 행동에 대해서는 상태가 변하지 않음)
      • $p(6,-1 | 5,right) = 1$
      • $p(7,-1 | 7,right) = 1$
      • $p(10,r | 5,right) = 0$
    • 이것은 할인이 없는, episodic task 이다.
    • 모든 전이에 대한 보상은 -1 이며, terminal state 에 닿을 때까지 지속된다.
    • terminal state 는 해당 그림에서 음영으로 표시된 상태이다.
    • 모든 상태 $s, s’$ 와 행동 $a$ 에 대한 기대 보상 함수는 $r(s,a,s’) = -1$ 이다.
    • 에이전트가 equprobable random policy (모든 action 이 동등 확률) 을 따른다고 가정한다.

• Policy Improvement

  • 예제 4.1 gridworld 의 iterative policy evaluation 의 수렴

  • 정책의 변경
    • 임의의 결정론적 정책 $\pi$ 에 대한 가치함수 $v_\pi$ 를 결정했다고 가정할 경우,
    • 일부 상태의 경우 결정론적으로 행동 $a \neq \pi (s)$ 인 a 를 선택하도록 정책을 변경해야 하는지 여부를 알고 싶음
    • 우리는 $s$ 상태에서 현 정책을 따르는 것이 얼마나 좋은지 ($v_\pi (s)$) 를 알고 있지만, 새 정책으로 변경하는 것이 더 나은지 알고 싶음
    • 위 질문에 대한 하나의 해법은 $s$ 상태에서 $a$ 를 선택하고, 그 뒤 기존 정책 $\pi$ 를 따라보는 것이다.

    

    • 그 값은 위와 같다.
    • 위의 값이 $v_\pi (s)$ 보다 큰지 작은지가 중요하다.
      • 클 경우, $s$ 에서 $a$ 를 선택한 뒤 $\pi$ 정책을 따르는 것이 $\pi$ 를 계속 따르는 것보다 낫다는 뜻임.
      • 즉, $s$ 에서 $a$ 를 선택하는 정책이 $\pi$ 정책보다 더 나은 정책임.
      • 이것을 정책 개선 정리 (policy improvement theorem) 라 한다.
    • $\pi$ 와 $\pi’$ 를 결정론적 정책이라 가정, $\textrm{all s} \in S$ 인 경우

    

    • 정책 $\pi’$ 는 $\pi$ 와 같거나 보다 좋은 정책이다.

    

    • 모든 상태에서 위 4.7이 성립할 경우 4.8 또한 성립한다.

    

    • 위와 같이 하나의 상태에서 특정 행동을 변경하는 정책을 어떻게 평가하는지 알아봤음.
    • 이 방식을 모든 상태에 모든 선택가능한 행동에 적용하는 것으로 확장하는 것은 자연스러운 방법이다.
    • 즉, 새로운 탐욕 정책 $\pi’$ 를 고려해본다.

  • Policy Improvement

    

    • $\arg\max_a$ 는 뒤의 식이 최대값이 되는 $a$ 를 뜻한다. (동률일 경우 임의로 선택)
    • greedy policy 는 $v_\pi$ 하의 단기적으로 가장 좋아보이는 행동을 선택한다. (한 번의 스텝 진행만을 고려)
    • greedy policy 는 policy improvement theorm (4.7) 의 조건을 만족하므로, 기존 정책과 같거나 더 좋은 정책이라는 것을 알 수 있다.

    • 기존 정책의 가치 함수를 사용하여 기존의 정책보다 더 나은 정책을 만드는 것을 policy improvement 라 한다.

    • new greedy policy $\pi’$ 가 old policy $\pi$ 만큼 좋지만, 더 좋지는 않은 상태를 가정한다.
      • for $\textrm{all s} \in S$
      • $v_\pi = v_{\pi’}$
      • 4.9 의 식을 따름
    • 결국 위의 식은 Bellman optimality equation 이 된다.
    • 따라서 $v_{\pi’}$ 는 $v_*$ 와 같고 $\pi$ 와 $\pi’$ 는 최적 정책 (optimal policy) 이 된다.
    • 정책 개선 (Policy Improvement) 는 기존 정책이 이미 최적이 아닌 경우, 엄격하게 더 나은 정책을 제공한다.
  • 확률론적 정책 (stochastic policy) 의 경우
    • 지금까지 결정론적 정책 (deterministic policy) 의 경우를 고려하였음.
    • 일반적인 경우 확률론적 정책 (stochastic policy) $\pi$ 는 확률에 특화되어 있다.
    • $\pi (a|s)$ : $s$ 상태에서 $a$ 행동을 선택할 확률
    • policy improvement theorem 은 사실 확률론적 정책으로 쉽게 확장이 가능하다.
      • 최선의 행동이 복수개일 경우 특정 확률의 배분을 차지할 수 있다.
      • 차선의 행동은 확률이 0 가 된다.
      • (예제 4.1 gridworld 의 iterative policy evaluation 의 수렴 참조)

• Policy Iteration

  • Policy Iteration
    • 정책 $\pi$ 에서 $v_\pi$ 를 이용해 더 나은 정책 $\pi’$ 를 도출했다면..
    • $v_{\pi’}$ 를 계산하여 더 나은 정책 $\pi’’$ 를 도출할 수도 있다.
    • 따라서, 우리는 단조롭게 개선되는 일련의 정책과 가치 함수를 얻을 수 있다.

    

    • $\overset{E}{\rightarrow}$ 는 policy evaluation 을,
    • $\overset{I}{\rightarrow}$ 는 policy improvement 를 뜻한다.
    • 각 정책은 이전의 정책보다 엄격히 개선되었다는 것을 보장한다. (이미 최적이 아닌 경우)
    • 유한 MDP 는 유한한 수의 정책을 가지고 있기 때문에, 이 프로세스는 반드시 최적 정책과 최적 가치함수에 유한한 반복 진행으로 수렴한다.
    • 위의 방법으로 최적 정책을 찾는 방법을 policy iteration 이라 한다.

    

    • 반복 계산인 각 정책 평가 (policy evaluation) 은 이전 정책에 대한 가치 함수로 시작된다.
    • 이것은 수렴의 속도를 크게 향상시키는데, 이전 정책에서 다음 정책으로 변화 할때, 가치 함수가 크게 바뀌지 않기 때문으로 추정된다.
• 예제 4.2 : Jack’s Car Rental
  • 문제의 설정
    • Jack 은 렌터카 회사의 두 지점을 관리한다.
    • 매일 일정 수의 고객이 자동차를 렌트하기 위해 각 지점에 도착한다.
      • 사용할 수 있는 자동차가 있으면 그것을 임대하고 $10 을 정립한다.
      • 지점에 차가 없으면 사업을 잃게 됨
    • 차량은 반납한 다음날부터 대여가 가능함
    • 차량이 필요한 곳에서 사용될 수 있도록, 두 지점간 차량을 밤 사이에 이동시킬 수 있고, 차량 당 $2 가 든다.
      • 한 위치에서 차량을 최대 5대 까지 이동할 수 있음
    • 각 위치에서 요청되고 반환되는 자동차의 수는 푸아송 확률 변수라고 가정한다.
      • 즉, 수량이 $n$ 일 확률은 $\frac{n!}{\lambda^n} e^{-\lambda}$ 이며, $\lambda$ 는 예상치이다.
      • $\lambda$ 를, 첫 번째 위치와 두 번째 위치 각각, 3과 4 (렌탈 수량), 3과 2 (반납수량) 으로 가정한다.
    • 각 지점에 차량이 최대 20대까지 있을 수 있음 (추가되는 차량은 사라짐)
    • 할인율 $\gamma = 0.9$
      • 할인율을 이용해 연속적인 유한 MDP 로 가정
    • 하나의 step 기준은 하루
    • States 는 하루가 끝날 때 각 위치의 자동차 수
    • Actions 는 숫자 (밤 새 두 장소 사이를 오가는 차량의 수)
  • 하기 이미지는 차를 전혀 움직이지 않는 정책부터 시작하여, 정책 반복으로 찾은 정책의 순서를 보여준다.

  

  • Jack 의 자동차 임대 문제에 대한 정책 반복으로 찾은 정책의 순서와 최종 상태가치 함수
  • 각 상태에 대해 몇 대의 차를 보내야 하는지를 보여줌 (음수는 두번째 위치에서 첫 번째 위치로의 이동을 나타냄)
  • 각 정책은 이전 정책에서의 엄격한 개선을 한 것이며, 마지막 정책이 최적 정책임.
• Value Iteration
  • 정책 반복의 문제점
    • 정책 반복의 한 가지 단점은, 각 반복에 정책 평가가 포함된다는 점이다.
    • 정책 평가는 상태 세트를 여러 번 스윕하는 장 기간의 반복 계산일 수 있다.
    • 반복적인 정책 평가를 하면 $v_\pi$ 로의 수렴은 극한에서만 일어난다.
    • 그림 4.1 의 예는 정책 평가를 생략하는 것이 가능할 수 있음을 시사한다. (3번의 반복 이후에 greedy policy 에 영향을 주지 않음.)
  • 가치 반복 (Value Iteration)
    • 정책 반복 (Policy iteration) 의 정책 평가 (Policy evaluation) 단계는 정책 반복의 수렴 보장을 유지한 채 여러 가지 방법으로 축소될 수 있음.
    • 한 가지 중요한 특수 사례는 정책 평가 (Policy evaluation) 가 단 한번의 스윕 (각 상태의 업데이트 1회) 후에 중지되는 경우임.
    • 위와 같은 사례 (알고리즘) 를 Value Iteration 이라 한다.
    • 정책 개선 (Policy improvement) 과 축소된 정책 평가 (Policy evaluation) 는 단순한 업데이트 연산으로 결합할 수 있다.

    

    • 정책 평가와 같이, Value Iteration 도 정확한 $v_*$ 로의 수렴을 위해 무한히 반복을 해야 한다.
    • 실제로는, 가치 함수가 한 번의 스윕에서 매우 적은 양만 변화할 경우 중지한다.
    • 아래의 박스는 완성된 알고리즘 (중지 상태를 포함) 을 보여준다.

    

    • 가치 반복 (Value Iteration) 은 각 스윕에서 한 번의 정책 평가 스윕과 한 번의 정책 개선 스윕을 효과적으로 결합한다.
    • 종종 각 정책 개선 (Policy Improvement) 스윕 사이에 여러 정책 평가 (Policy evaluation) 스윕을 삽입하여 달성된다.
    • 일반적으로 축소된 정책 반복 알고리즘의 전체 클래스는 일부는 정책 평가 (Policy evaluation) 업데이트, 일부는 가치 반복 (Value Iteration) 업데이트 를 사용하는 스윕 시퀀스로 생각할 수 있다.
      • 4.10 수식의 최대 (max) 연산이 유일한 차이점이기 때문
      • 즉, 정책 평가의 일부 스윕에 최대 (max) 연산 작업이 추가됨을 의미함
    • 이러한 모든 알고리즘은 할인된 유한 MDP 에 대한 최적의 정책으로 수렴함.
  • 예제 4.3 : Gambler’s Problem
    • 문제
      • 도박꾼은 일련의 동전 던지기 결과에 대해 베팅할 기회가 있다.
      • 동전이 앞면이 나오면 그는 걸었던 만큼의 달러를 얻고, 뒷면이면 지분을 잃는다.
      • 도박꾼이 $100 의 목표에 도달하면 이기고, 돈을 다 잃으면 끝나게 된다.
      • 매번 도박꾼은 자신의 자본 중 어느 정도를 걸어야 할 지 정해야 한다.
      • 이 문제는 할인되지 않은, 에피소딕한 유한한 MDP 로 공식화될 수 있다.
    • 정의
      • 상태 : 도박꾼의 자본, $s \in \lbrace 1,2,…,99 \rbrace$
      • 행동 : 베팅 금액, $a \in \lbrace 0, 1, …, min(s, 100-s) \rbrace$
      • 보상 : 도박꾼이 목표에 도달하였을때 +1, 그 외 모든 전환에서 0
      • 상태가치 함수는 위의 경우 각 상태에서 승리할 확률을 제공한다.
      • 정책은 자본과 베팅 금액 간 매핑이다.
      • 최적의 정책은 목표에 도달할 확률을 최대화한다.
      • $p_h$ : 동전이 앞면이 나올 확률
      • $p_h$ 를 알게 되면, 전체 문제를 알 수 있고, 가치 반복 (Value Iteration) 등으로 풀 수 있다.
      • 그림 4.3 은 가치 반복의 연속적인 스윕에 대한 가치 함수의 변화를 보여준다.
      • 그림 4.3 은 $p_h = 0.4$ 인 경우 최적 정책을 보여준다. 이 정책은 최적이지만 고유하지는 않다.
        • 최적 가치 함수 상 값이 동률일 경우…

      

• Asynchronous Dynamic Programming
  • 기존 DP 모델의 한계
    • MDP 의 전체 상태 집합에 대한 연산을 포함한다.
    • 즉, 상태 집합 전체에 대한 스윕이 필요함.
    • 상태 세트가 매우 크면 한 번의 스윕도 엄청난 비용일 수 있다.
    • 백게먼 게임에서 상태의 수는 $10^{20}$ 개 이다.
    • 이는 초당 백만 개의 상태의 가치 반복 업데이트를 수행할 수 있더라도, 단일 스윕을 완료하는 데 천 년 이상이 걸린다.
  • 비동기식 DP 알고리즘
    • 비동기식 DP 알고리즘은 상태 세트의 체계적 스윕이 구성되지 않은 내부 반복 DP 알고리즘이다.
    • 이 알고리즘은 사용 가능한 다른 상태의 값을 사용하여 순서에 관계없이 상태 값을 업데이트한다.
      • 일부 상태 값은 다른 상태 값이 업데이트 되기 전에 여러 번 업데이트 될 수 있다.
      • 그러나 올바른 수렴을 위해 모든 상태의 값을 계속 업데이트 해야한다.
      • 일정 시점 이후에는 어떤 상태도 무시할 수 없다.
  • 비동기식 DP 알고리즘의 이점
    • 비동기 DP 알고리즘은 업데이트할 상태를 선택하는 데 큰 유연성을 제공한다.
      • 예를 들어 가치 반복 업데이트 (4.10) 를 이용하여, 매 스탭 $k$ 에 대해 하나의 상태인 $s_k$ 에 대해서만 업데이트 하는 것이다.
      • 만약, $0 \leq \gamma < 1$ 일 경우, $v_*$ 에 대한 점근적인 수렴은 모든 상태가 시퀀스 $\lbrace s_k \rbrace$ 에서 무한한 횟수로 발생하는 경우에만 보장된다.
        • 시퀀스가 확률적일 수도 있음
        • 할인되지 않는 에피소드 케이스의 경우, 수렴되지 않는 일부 업데이트 순서가 있을 수 있지만 이는 상대적으로 피하기 쉬움)
      • 마찬가지로 정책 평가와 가치 반복 업데이트를 혼합하여 일종의 비동기식 축소된 정책 반복을 생성할 수 있음
      • 이것과 다른 더 특이한 DP 알고리즘에 대한 세부 사항은 이 책의 범위를 벗어남
      • 몇 가지 다른 업데이트가 다양한 Sweepless DP 알고리즘에서 유연하게 사용할 수 있는 빌딩 블록을 형성한다는 것은 분명함
      • 스윕을 피한다고 해서 반드시 적은 계산으로 벗어날 수 있다는 의미는 아님.
        • 이는 알고리즘이 정책을 개선하기 전에 절망적으로 긴 스윕에 갇힐 필요가 없음을 의미함
      • 알고리즘의 진행률을 향상시키기 위해 업데이트를 적용할 상태를 선택하여 이러한 유연성을 활용할 수 있음.
        • 값 정보가 상태에서 상태로 효율적으로 전파되도록 업데이트 순서를 정할 수 있음
        • 일부 상태는 다른 상태만큼 자주 값을 업데이트할 필요가 없을 수 있음
        • 최적의 동작과 관련이 없는 경우 일부 상태를 완전히 업데이트 하지 않을 수도 있음
    • 비동기식 알고리즘을 사용하여 실시간 상호작용 내용을 더 쉽게 혼합하여 계산할 수 있다.
      • MDP 를 풀기 위해 에이전트가 실제로 MDP 를 경험하는 동안, 동시에 반복 DP 알고리즘을 수행할 수 있다.
      • 에이전트의 경험은 DP 알고리즘이 업데이트를 적용할 상태를 결정하는 데 사용할 수 있다.
      • 동시에 DP 알고리즘의 최신 값과 정책 정보를 이용해 에이전트의 의사 결정에 활용할 수 있다.
        • 예를 들어 에이전트가 특정 상태를 방문할 때 상태에 업데이트를 적용할 수 있다.
        • 이를 통해 에이전트와 가장 관련성 높은 상태 세트 부분의 업데이트에 집중할 수 있다.
• Generalized Policy Iteration
  • 정책 반복 (Policy Iteration) 에 대한 내용 정리
    • 정책 반복은 두 개의 동시 상호 작용 프로세스로 구성됨
      • 현재 정책과 일치하는 가치 함수를 만들기 (정책 평가)
      • 현재 가치함수와 관련하여 정책을 탐욕스럽게 만들기 (정책 개선)
    • 정책 반복 : 이 두 프로세스는 서로 번갈아가며 다른 프로세스가 시작되기 전에 완료됨
    • 가치 반복 : 각 정책 개선 사이에 정책 평가의 단일 반복만 수행됨
    • 비동기식 DP 방법 : 평가 및 개선 프로세스가 훨씬 더 세밀하게 끼워넣어짐
      • 예 : 다른 프로세스로 돌아가기 전에 한 프로세스에서 단일 상태가 업데이트됨
    • 두 프로세스가 계속해서 모든 상태를 업데이트 하는 한, 궁극적인 결과는 일반적으로 최적 가치 함수와 최적 정책으로 수렴됨.
  • Generalized Policy Iteration (GPI) : 일반화된 정책 반복
    • 우리는 일반화된 정책 반복 (GPI) 이라는 용어를 사용하여 정책 평가 및 정책 개선 과정이 서로 상호작용하는 일반 아이디어를 나타낸다.
      • 두 과정의 세부 사항과 세분화와는 독립적인 개념임.
    • 거의 모든 강화학습 방법은 GPI로 잘 설명되어 있음.

    

    • 즉, 모든 것들은 식별 가능한 정책과 가치 함수를 가지며, 정책은 항상 가치 함수에 대해 개선되고, 가치 함수는 항삭 정책에 대한 가치 함수로 향하도록 조정된다.
    • 만약 평가 과정과 개선 과정이 모두 안정화 되면, 즉 더 이상 변화가 발생하지 않으면, 가치 함수와 정책은 최적이어야 한다.
    • 가치 함수는 현 정책과 일치할 때에만 안정화 되고, 정책은 현 가치함수에 대해 탐욕스러울 경우에만 안정화 된다.
    • 따라서 두 과정이 모두 안정화되려면, 자신의 평가 함수에 대해 탐욕스러운 정책을 찾아야 한다.
    • 이는 벨만 최적 방정식 (4.1) 이 성립하며, 정책과 가치함수가 최적임을 의미한다.

    

    • GPI 의 평가 및 개선 프로세스는 경쟁과 협력으로 볼 수 있음
      • 정책을 가치 함수에 대해 탐욕스럽게 만들면 일반적으로 가치 함수가 변경된 정책에 대해 부정확해짐
      • 가치 함수를 정책과 일치하게 만들면 해당 정책이 더 이상 탐욕스러운 정책이 아니게 됨.
      • 장기적으로 이 두 과정은 하나의 공통해결책인 최적의 가치 함수와 최적의 정책을 찾기 위해 상호작용함.
    • 위 다이어그램에서 제안된 대로 2차원 공간의 두 개의 선으로 생각해볼 수 있음.
      • 실제 기하학은 이보다 훨씬 복잡하나, 이 다이어그램은 실제 상황이 어떤 식으로 일어나는지를 시사함.
      • 각 과정은 가치함수, 정책을 두고 두 목표중 하나의 해결책을 나타내는 선으로 이끈다.
      • 두 목표는 직교하지 않기 때문에 목표 간 상호작용이 발생 (한 목표로 직접적으로 나아가면 다른 목표에서 멀어지는 움직임)
      • 그러나 결국 공동 프로세스는 최적의 목표에 가까워지게 된다.
      • GPI 에서 각 목표에 대해 작고 불완전한 단계를 취할 수도 있으나, 어느 경우에도 두 과정은 전반적인 최적의 목표를 달성하기 위해 함께 작동한다.
• Efficiency of Dynamic Programming
  • MDP 문제에서 DP 방식이 가지는 효율성
    • DP(Dynamic Programming)는 매우 큰 문제에는 적합하지 않을 수 있지만, MDP(Markov Decision Processes)를 해결하기 위한 다른 방법과 비교하면 DP 방법은 실제로 꽤 효율적임.
    • 일부 기술적인 세부 사항을 무시한다면, DP 방법이 최적 정책을 찾는 데 걸리는 (최악의 경우) 시간은 상태와 액션의 수에 다항식으로 표현됨.
      • n과 k가 상태와 액션의 수를 나타낸다면, DP 방법은 n과 k의 다항식 함수보다 적은 계산 작업을 필요로 함.
      • DP 방법은 전체 정책의 수가 $k^n$ 인 것과는 상관없이 다항 시간 내에 최적 정책을 찾을 것을 보장함.
      • (직접 탐색 (모든 경우의 수, 가능한 정책을 검사하고 평가) 은 동일한 보장을 제공하기 위해 각 정책을 철저히 검사해야 함)
    • 일부의 경우 선형 프로그래밍 방법 (문제를 선형 제약 조건과 목적함수를 활용해 수학적으로 리모델링) 도 MDP를 해결하는 데 사용될 수 있으며, DP 방법보다 수렴 보장이 더 좋을 수 있음.
      • 예를 들어, MDP 문제에서 상태 공간이 크고 액션 수가 상대적으로 작은 경우
      • 혹은 작은 상태 수
    • 그러나 가장 큰 문제에 대해서는 DP 방법만이 실현 가능함.
      • DP(Dynamic Programming)은 종종 차원의 저주(curse of dimensionality)라는 이유로 적용 가능성이 제한적으로 생각되기도 한다. 이는 상태 변수의 수에 따라 상태의 수가 지수적으로 증가하기 때문.
      • 큰 상태 집합은 어려움을 일으킬 수 있지만, 이는 문제의 본질적인 어려움이며 DP 자체의 해결 방법의 어려움은 아니다.
      • 실제로 DP는 직접 탐색이나 선형 프로그래밍과 같은 경쟁적 위치의 방법들보다 큰 상태 공간을 처리하는 데 더 적합함.
  • 비동기 DP 의 활용방식
    • 실제로 DP(Dynamic Programming) 방법은 오늘날의 컴퓨터를 사용하여 수백만 개의 상태를 가진 MDP(Markov Decision Process)를 해결하는 데에 사용될 수 있다.
    • 정책 이터레이션(policy iteration)과 가치 이터레이션(value iteration) 모두 널리 사용되며, 일반적으로 어떤 것이 더 우수한지 명확하지 않음.
    • 이러한 방법들은 보통 좋은 초기 값 함수 또는 정책으로 시작되었을 때, 이론적인 최악의 경우 실행 시간보다 훨씬 빠르게 수렴함.
    • 상태 공간이 큰 문제에서는 비동기적인 DP 방법이 종종 선호됨.
    • 동기적인 방법의 경우 하나의 전체 순회를 완료하기 위해서는 모든 상태에 대한 계산과 메모리가 필요함.
    • 일부 문제에서는 심지어 이 정도의 메모리와 계산도 실용적이지 않을 수 있지만, 최적 해결 경로에는 상대적으로 적은 수의 상태가 발생할 수 있으므로 문제는 여전히 해결이 가능함.
    • 비동기적인 방법과 GPI의 다른 변형들은 이러한 경우에 적용될 수 있으며, 동기적인 방법보다 좋거나 최적의 정책을 훨씬 빠르게 찾을 수 있음.

Policy Evaluation (Prediction)

• Policy Evaluation vs. Control

  • 학습 목표
    • 정책 평가 (policy evaluation) 와 제어 (control) 의 구분
    • 동적 프로그래밍 (Dynamic Programming) 이 적용될 수 있는 설정(환경) 과 제한을 이해
  • Policy Evaluation 과 Control 의 정의
    • Policy Evaluation : 주어진 정책에 대한 stable 한 가치 함수를 구하는 것 (얼마나 좋은지 평가)
      • $\pi \to v_\pi$
      • $v_\pi (s) \doteq E_\pi [ G_t | S_t = s]$
      • $G_t \doteq \sum_{k=0}^\infty \gamma^k R_{t+k+1}$
        • 리턴 값은 미래의 보상에 대한 할인된 합계이다.

    • Control : 가치 함수를 통해 가장 많은 보상을 얻는 정책을 찾는 것 (정책을 발전시키는 것)

      

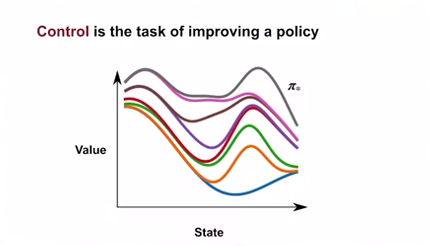
      • 모든 상태에서의 가치가 같거나 더 나은 정책을 찾는 것
      • 반복적으로 찾다 보면 최적의 정책을 찾게 됨.

  • Dynamic Programming Algorithms

    • 벨만 방정식을 사용해 가치 평가와 제어의 반복적인 알고리즘을 정의하는 것

  

  • Linear equations 와 Dynamic Programming 비교
    • Linear equations
      • 가치함수 $v_\pi$ 를 찾기 위해, 각 상태별로 위의 하나의 방정식을 갖게 된다.
    • Dynamic Programming
      • 통상 MDP 의 문제에서 DP 방식이 보다 더 적절한 방식이다.

      

      • DP 에서는 다양한 형태의 벨만 방정식을 사용한다.
      • 위의 경우 환경역학 $p$ 에 대한 지식을 기반으로 한다.
      • 고전적인 DP 에서는 환경과의 상호작용을 포함하지 않는다. (대신 주어진 MDP 모델을 활용 / 함수 $p$ 에 접근할 수 있다는 가정.)
      • 대부분의 강화학습 알고리즘은 모델이 없는 DP 의 근사화된 프로그래밍이라고 볼 수 있다.
      • (이러한 특징은 이후에 소개할 Temporal different space dynamic planning algorithm 에서 두드러진다.)

• Iterative Policy Evaluation

  • 학습목표
    • 주어진 정책에서 상태값 평가를 위한 반복 정책 평가 (iterative policy evaluation) 알고리즘의 개요
    • 반복 정책 평가 (iterative policy evaluation) 를 적용하여 가치함수 계산
  • 벨만 방정식과 Iterative Policy Evaluation 간의 관계
    • DP 알고리즘은 벨만 방정식을 업데이트 룰로 변경함으로써 얻을 수 있다.
    • iterative policy evaluation 알고리즘 또한 이러한 알고리즘 중 하나이다.

    

    • 벨만 방정식 중 $v_\pi$ 에 대핸 재귀적 표현을 활용한다.
    • 업데이트 룰에서는 참 가치함수가 아닌 예측 값을 활용한다.
      • 이 방식은 점진적으로 보다 나은 대략적인 가치 함수를 제공하게 된다.

      

      • 각각의 반복은 모든 상태 집합에 대해 업데이트를 적용하는데, 이를 스윕 (sweep) 이라고 한다.
      • 만약 모든 상태에 대해, 가치 함수 근사값 $v_k$ 와 $v_{k+1}$ 의 값이 같을 경우 정책에 대한 참 가치 함수를 찾았다고 한다.
      • ${v_0}$ 가 어떤 값이여도, $k$ 가 무한대에 수렴하면, $v_k$ 또한 $v_\pi$ 로 수렴하게 된다.
  • 구현의 방식

    • 2개의 배열 사용

      

      • 모든 상태 세트에 대해 업데이트를 진행한다.
      • Old value V 를 이용해 New value V’ 를 갱신한다.
      • Old value V 는 업데이트 중에 변동이 없다.
      • 모든 상태를 순회, 업데이트 후에 V’ 를 V 에 할당하고, V’ 에 다시 업데이트를 진행한다.

    • 1개의 배열 사용

      

      • V 배열만을 이용해 업데이트를 진행한다.
      • 경우에 따라 특정 상태의 값을 참조할 때, Old value 가 아닌 New value 를 참조하기도 한다.
      • 이러한 한 개의 배열 버전 또한 수렴을 보장하며, 사실 보통의 경우 최신 값을 사용하기에 더 빠르게 수렴한다.

    • 여기에서는 단순성을 위해 2개의 배열 버전에 집중한다.

  • Iterative Policy Evaluation 의 예시
    • 4 x 4 의 grid world 를 가정
    • 좌측 상단과 우측 하단에 Terminate State 가 있는 Episodic MDP 로 정의
    • 모든 상태이동의 보상은 -1
    • 할인 값은 없다고 가정 ($\gamma = 1$)
    • 각 상태별로 4개의 방향으로 이동할 수 있음 (up, down, left, right). 각 행동은 결정론적임 (확률=100%)
    • 그리도 밖으로의 이동은 에이전트가 해당 상태에 그대로 머물도록 함
    • 정책은 uniform random policy (각 확률 25%).

    

    • 스윕은 좌에서 우로, 위에서 아래로 진행된다.
    • 첫 스윕 결과는 위의 식에 의해 Terminal State 를 제외하고 모두 -1 이 된다.
    • 첫 풀 스윕 이후 V’ 을 V 로 카피하고, 위 과정을 반복한다.

    

    • 위는 iterative policy evaluation 의 전체 알고리즘이다.
    • 각 상태의 이전과 이후의 차이 ($\delta$) 가 정의한 작은 숫자 ($\theta$) 보다 작을 경우 루프를 중지한다.
    • $\theta$ 가 충분히 작을 경우, V 는 $v_\pi$ 에 가까운 값이라 할 수 있다.

    

Policy Iteration (Control)

• Policy Improvement

  • 학습목표
    • 정책 개선 이론 (policy improvement theorem) 이해하기
    • 주어진 MDP 에서 더 나은 정책의 생성을 위해 정책에 가치함수 적용하기

  • Policy Improvement

    

    • 최적 가치함수 $v_*$ 에 대해 greedy action 을 취한 정책을 최적 정책 (Optimal Policy) 이라 한다.
    • 임의의 정책 $\pi$ 를 따르는 가치 함수 $v_\pi$ 에 대해 greedy action 을 $v_\pi$ 에 대한 탐욕 정책이라 했을 때…
    • 현재의 정책 $\pi$ 와 위의 정책이 차이가 없을 경우 $\pi$ 는 이미 $v_\pi$ 에 대한 탐욕 정책이며,
    • 이 경우 $v_\pi$ 가 벨만 최적성 방정식을 따른다면, $\pi$ 는 최적 정책이다.
  • Policy Improvement Theorem
    • $\pi$ 가 최적정책이 아니라면, $\pi$ 보다 엄격한 개선이 이루어진 새로운 정책이 존재한다.
    • $q_\pi (s, \pi’(s)) \geq q_\pi (s, \pi (s))$ for all $s \in S$ $\to \pi’ \geq \pi$

    

    • uniform random policy 를 따르는 $v_\pi$ 가치함수에 대해, greedy policy $\pi’$ 이 Policy Improvement Theorem 에 의해 더 개선된 정책임.
    • Policy Improvement Theorem 은 새로운 정책이 이전 정책보다 개선된 정책임 만을 보장한다.
      • 개선된 정책이 최적 정책임은 보장하지 않음 (가치함수가 최적 가치함수가 아님)

• Policy Iteration

  • 학습목표
    • 최적 정책을 찾기 위한 정책 반복 알고리즘 (policy iteration algorithm) 을 정의하기
    • “the dance of policy and value” (평가와 개선을 반복하여 최적 정책을 찾는 것) 이해하기
    • 정책 반복 (policy iteration) 을 적용하여 최적 정책과 최적 가치 함수 계산하기

  • Policy Iteration

    

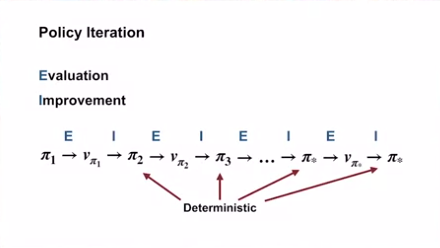
    • 더 이상 가치 함수를 통한 정책이 변경되지 않으면 그것이 최적 정책이다.
    • 결정론적 정책을 사용하기에, 필연적으로 최적 정책에 도달한다.

    

    • $\pi_1$ 에 대한 가치함수 $v_{\pi_1}$ 을 구하면, $\pi_1$ 은 더이상 greedy policy 가 아니게 되고…
    • greedy policy $\pi_2$ 를 구하면 더 이상 가치함수 $v_{\pi_1}$ 이 정확한 가치함수가 아니게 된다.
    • 위의 과정을 반복하면 필연적으로 변하지 않는 정책 $\pi_*$ 와 정확한 가치함수 $v_*$ 를 구하게 된다.

    

    • 4x4 gridworld 예제의 정의

    

    • $\pi_0$

    

    • $v_{\pi_0}$

    

    • $\pi_1$

    

    • $v_{\pi_1}$

    

    • $\pi_2$

    

    • $v_{\pi_2}$

    

    • $\pi_3$

    

    • $\pi_*$

    

    • The Power of Policy Iteration

    

    • 최적 정책에 도달하기 전까지, 계속적으로 정책이 개선됨을 볼 수 있다.
    • 최적 정책이 선형적이지 않을 때도 정책에 도달할 수 있다.

Generalized Policy Iteration

• Flexibility of the Policy Iteration Framework

  • 학습목표
    • 일반화된 정책 반복 프레임워크 (framework of generalized policy iteration) 이해하기
    • 가치 반복 (value iteration) 과 일반화된 정책 반복 (generalized policy iteration) 의 주요 예시
    • 동기 (synchronous) / 비동기 (asynchronous) 동적 프로그래밍 방법 간 차이점을 이해하기

  • 유연한 Policy Iteration

    

    • 현 정책에 가까운 가치 함수 예측치를 사용
    • 좀 더 탐욕적인 정책을 사용하나, 완전히 탐욕적인 정책은 아닌 정책을 사용
    • 이러한 진행 또한 최적 정책과 최적 가치함수를 향해 나아간다.
    • 이러한 Policy Iteration 을 Generalized Policy Iteration 이라고 함.
  • Value Iteration
    • Generalized Policy Iteration 중 하나
    • 모든 상태를 sweep 하고, 현 가치 함수에 대해 탐욕 정책을 사용하는 것은 같음.
    • 그러나, 완전한 정책 평가를 하는 것은 아님
      • 모든 상태에 대해 단 한번의 스윕만을 진행
      • 스윕 진행 후 다시 탐욕 정책을 사용함.

    

    • 이러한 업데이트 룰을 상태 가치함수에 바로 적용한다.
      • $V(s) \gets \max_a \sum_{s’,r} p(s’,r|s,a) [r + \gamma V(s’) ]$
      • 업데이트가 어떠한 특정 정책을 참조하지 않기 때문에, 이 방식을 value iteration 이라 한다.
    • 이 방식은 iterative policy evaluation 과 매우 유사한데, 고정된 정책을 이용해 업데이트 하는 것이 아닌, 현재의 추정 값을 이용해 최대화 하는 것이 특징이다.
    • value iteration 또한 극한 값에서 $v_*$ 에 수렴한다.
    • 우리는 극한으로 진행될 때까지 기다릴 수 없으므로, 종료 조건을 둔다.
    • 최종적으로 구해진 최적 가치 함수에 대해 $\arg\max$ 를 취함으로서 최적 정책을 얻게 된다.
  • Avoiding full sweeps
    • Synchronous DP
      • value iteration 또한 policy evaluation iteration 과 마찬가지로 모든 상태를 (순차적으로) 스윕한다.
      • 시스템 적으로 스윕을 하는 방식을 synchronus (동기 방식) 라 한다.
      • 만약 상태공간이 크다면, 이러한 방식은 문제가 된다.
        • 모든 스윕 단계에 매우 긴 시간을 소모함
    • Asynchronous DP
      • 상태의 값을 특정 순서 없이 업데이트 한다. (시스템 적인 스윕이 아님).
      • 다른 상태값이 한번 업데이트 되는 동안 특정 상태값을 여러 번 업데이트 할 수 있음.
      • 수렴을 보장하기 위해서는, 계속하여 모든 상태의 값을 업데이트 해야함.
        • 예를 들어 다른 상태를 무시하고 3개의 상태값만 계속 업데이트 한다면, 다른 상태의 값이 옳을 리가 없기 때문에 수렴할 수가 없음.
      • 이러한 선택적 업데이트 덕분에, 값 정보를 빠르게 전파할 수 있음.
        • 어떠한 경우에서는 시스템적인 스윕보다 더 효율적일 수 있음.
          • 예를 들어 최근 값이 변한 상태의 주변 값들을 집중적으로 업데이트.

• Efficiency of Dynamic Programming

  • 학습목표
    • 최적 정책을 찾기 위한 대안으로서의 무작위 탐색 방법 (brute force search) 설명
    • 가치 함수 학습을 위한 대안으로서의 몬테카를로 (Monte Carlo) 방식 설명
    • 최적 정책 탐색에 있어서 동적 프로그래밍 (Dynamic programming) 과 부트스트래핑 (bootstrapping) 방식이 대안 전략과 비교하여 가지는 이점을 이해하기
  • A Sampling Alternative for Policy Evaluation (Monte Carlo)
    • Dynamic Programming 의 policy evaluation iteration 의 대안

    • Monte Carlo 방식

      

      • 정책 $\pi$ 에 대한 많은 리턴값을 수집하여 평균 값을 구하는 방식
      • 결국 값에 수렴하게 됨

      

      • 수렴을 위해서는 각 상태에 대한 많은 리턴 수집값이 필요
        • 이 값들은 $\pi$ 에 의해 선택된 random action, 환경 역학에 의한 random state transition 등 많은 random 성을 띄게 됨.
      • 이러한 과정을 모든 상태에 대해 별개로 진행해야 함.

    • Dynamic Programming 의 이점

      

      • Dynamic Programming 의 핵심은 각 상태의 평가를 별개의 문제로 취급할 필요가 없다는 점이다.
        • 이미 계산해 놓은 다른 상태의 값을 이용할 수 있음.
      • 이렇게 이후 상태의 추측값을 사용해 현재의 추측값을 개선하는 것을 부트스르래핑 (bootstrapping) 이라 한다.
        • 이 방식이 각각의 상태를 별개로 계산하는 몬테카를로 방식보다 훨씬 효율적임.
  • Brute-Force Search
    • Dynamic Programming 의 policy iteration 의 대안

    • Brute-Force Search 방식

      

      • 이 방식은 단순히 모든 결정론적인 정책을 하나하나 평가하여 가장 높은 값의 정책을 선택하는 것임.
      • 정책의 수는 유한하고, 언제나 최적 결정론적 정책은 존재함으로 최적 정책을 찾을 수 있음.
      • 그러나 결정론적인 정책의 수가 너무 많을 수도 있음.
        • 각각의 상태에 대해 하나의 행동을 선택해야 함.
          • $| \mathscr{A} | * | \mathscr{A} | * \cdots * | \mathscr{A} |$
        • 즉, 결정론적 정책의 수는 지수적이다.
          • ${| \mathscr{A} |}^{| \mathscr{S} |}$
      • 따라서 이 프로세스는 시간이 매우 오래 걸린다.
    • Policy Improvement Theorem 의 이점
      • 점점 더 나은 정책을 찾게 된다.
      • 이 점은 모든 정책에 대한 검색보다 훨씬 효율적이다.
  • Efficiency of Dynamic Programming
    • Policy Iteration : $| \mathscr{S} |$ 와 $| \mathscr{A}|$ 에 대한 다항식 곱의 복잡도
    • Brute-Force Search : ${| \mathscr{A} |}^{| \mathscr{S} |}$ 개의 정책
    • Dynamic Programming 은 Brute-Force Search 에 비해 지수적으로 빠름
      • 예를 들어 4x4 Grid World 의 경우 DP 는 위의 예시에서 약 5번의 스윕을 통해 최적 정책을 찾아냈으나, Brute-Force Search 의 경우 $4^{16}$ 개의 정책을 확인해야 함.
  • The Curse of Dimensionality (차원의 저주)
    • 관계된 요소의 수가 늘어날 수록 상태 공간의 크기가 지수적으로 늘어남
    • MDP 문제는 상태의 크기가 커질 수록 풀기 어려워짐
    • 하나의 에이전트가 Grid World 를 탐험하는 것은 괜찮지만, 대중교통을 설계하기 위해 몇천 명의 운전자가 수백 개의 지역을 돌아다니는 상태를 가정하면 어떻게 될까?
    • 사실 이는 Dynamic Programming 의 문제가 아닌 문제 자체의 내제된 복잡성이다.
• Warren Powell: Approximate Dynamic Programming for Fleet Management(Short)

• Warren Powell: Approximate Dynamic Programming for Fleet Management(Long)

• Week 4 Summary

  • Policy evaluation : 특정한 정책 $\pi$ 로부터 상태가치함수 $v_\pi$ 를 구하는 것
    • Iterative Policy Evaluation
      • $v_\pi (s) = \sum_a \pi (a|s) \sum_{s’} \sum_r p(s’,r | s,a) [ r+\gamma v_\pi (s’) ]$
      • $v_{k+1} (s) \gets \sum_a \pi (a|s) \sum_{s’} \sum_r p(s’,r | s,a) [ r+\gamma v_k (s’) ]$
      • $v_\pi$ 에 대한 벨만 방정식을 업데이트 룰로 바꾼 것
      • 반복 과정을 거치며 점점 더 근사하는 가치함수를 찾을 수 있음
  • Control : 정책을 발전시키는 과정
    • Policy improvement theorem
      • $\pi’ (s) \doteq \arg\max_a \sum_{s’} \sum_r p(s’,r | s,a) [ r+\gamma v_\pi (s’) ]$
      • 새로운 정책 $\pi’$ 는 현 가치함수에서 단순히 탐욕화한 정책이다.
      • $\pi’$ 은 $\pi$ 보다 엄격히 개선된 정책임을 보장한다. ($\pi$ 가 최적정책이 아닐 경우)
    • Policy Iteration
      • $E \to I \to \cdots \to E \to I \to v_* , \pi_*$
    • Generalized Policy Iteration
      • Policy Iteration 과 달리 Evaluation 과 Improvement step 을 끝까지 진행하지 않고 반복하는 것
        • value iteration : Generalized Policy Iteration 의 한 종류로, 모든 상태를 단 한번 스윕하고 정책을 개선시키는 것
      • asynchronous DP
        • 모든 상태를 시스템적으로 스윕하는 것이 아닌, 불규칙적인 방식으로 상태를 업데이트 하는 것
        • 모든 상태를 지속적으로 업데이트한다는 가정 하에 최적 정책으로 수렴하게 됨
        • 특정 상황에서 더 빠르게 수렴할 수 있으며, 상태 공간이 큰 문제에 효율적임
• Chapter Summary (RLbook2018 Pages 88-89)

Weekly Assessment

Course Wrap-up

• Bandits

  

  • 각 레버의 보상의 분포를 모르기 때문에, 각각의 arm 을 많이 시도하여 평균을 구해야 했었음.
  • Exploration - Exploitation Trade-Off
    • 지금 당장의 최선의 arm 을 당길 것인지, 다른 arm 을 탐험할 것인지?
  • Bandit 문제는 늘 같은 state 에서 action 을 선택하는 문제였음.
    • 불변하는 하나의 최상의 action 이 존재
    • 보상은 지연되지 않고 즉시 지급되었음

• MDP

  

  • Bandits 보다 복잡한 현실 문제를 더 잘 반영한 모델
  • 환경은 action 을 선택하였을 때 즉각적인 보상 뿐만 아니라 다음의 상태도 제공해 줌
    • 이 상태는 미래의 보상에 잠재적인 영향을 준다.
  • 보상은 미래에 받을 잠재적 보상값의 할인된 합계이다.
• Basic Concepts of Reinforcement learning
  • 정책 (policy) : 에이전트가 각 상태 (state) 에서 어떤 action 을 취할 것인지를 말함
  • 가치함수 (value function)
    • $v_\pi (s) \doteq E_{\pi} [ G_t | S_t = s ]$
    • 특정 정책 하에 각 상태에 대해 미래의 예상되는 리턴 값을 측정해줌
    • 혹은 특정 정책 하에 상태-행동 쌍에 대한 미래의 예상되는 리턴 값을 측정해줌
  • 벨만 방정식
    • 각 상태 혹은 상태-행동 쌍의 값을 가능한 다음 값과 연결 시켜주는 방정식 (부트스트래핑)

• Dynamic Programming

  

  • prediction (Policy Evaluation)
  • control (Policy Improvement)
  • Dynamic Programming 의 경우 환경 역학 (Environment dynamics) 에 접근할 수 있어야 한다.
  • 강화학습 문제, 혹은 현실의 문제에서는 이 환경역학에 접근할 수 없다. (시도해 보기 전엔 어떤 영향을 줄 지 알 수 없음.)
  • Dynamic Programming 은 강화학습 알고리즘의 핵심 기초가 된다.